设a1，a2，…，an为实数，证明：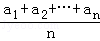
≤
．
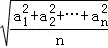见解析
【解析】
试题分析：利用排序原理，n个式子相加，可得n（a12+a22+…+an2）≤（a1+a2+…+an）2，上式两边除以n2，并开方可得结论．
证明：不妨设a1≤a2≤…≤an，则由排序原理得：
a12+a22+…+an2=a1a1+a2a2+…+anan
a12+a22+…+an2≤a1a2+a2a3+…+ana1
a12+a22+…+an2≤a1a3+a2a4+…+an﹣1a1+ana2
…
a12+a22+…+an2≤a1an+a2a1+…+anan﹣1．
将上述n个式子相加，得：n（a12+a22+…+an2）≤（a1+a2+…+an）2，
上式两边除以n2，并开方可得：
≤
．
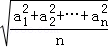科目：高中数学 来源：[同步]2014年新人教A版选修4-6 1.2最大公因数与最小公倍数 题型：选择题
已知7163=209×34+57，209=57×3+38，57=38×1=19，38=19×2．根据上述系列等式，确定7163和209的最大公约数是（ ）
A.19 B.2 C.38 D.57
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷（解析版） 题型：选择题
利用数学归纳法证明“（n+1）（n+2）…（n+n）=2n×1×3×…×（2n﹣1），n∈N*”时，从“n=k”变到“n=k+1”时，左边应增乘的因式是（ ）
A.2k+1 B.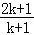
C.
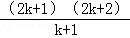D.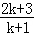
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.3排序不等式练习卷（解析版） 题型：解答题
若a1≤a2≤…≤an，而b1≥b2≥…≥bn或a1≥a2≥…≥an而b1≤b2≤…≤bn，证明：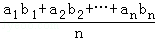
≤（
）•（
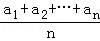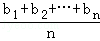）．当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.2一般形式柯西不等式练习卷（解析版） 题型：填空题
（2014•宿迁模拟）已知实数a1，a2，a3不全为零，正数x，y满足x+y=2，设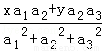
的最大值为M=f（x，y），则M的最小值为 ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.2一般形式柯西不等式练习卷（解析版） 题型：选择题
已知x，y，z∈R+且x+y+z=1则x2+y2+z2的最小值是（ ）
A.1 B.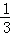
C.
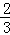D.2
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：选择题
二维形式的柯西不等式可用（ ）表示．
A.a2+b2≥2ab（a，b∈R）
B.（a2+b2）（c2+d2）≥（ab+cd）2（a，b，c，d∈R）
C.（a2+b2）（c2+d2）≥（ac+bd）2（a，b，c，d∈R）
D.（a2+b2）（c2+d2）≤（ac+bd）2（a，b，c，d∈R）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
时，第一步验证n=1时，左边应取的项是