
平面直角坐标系中,将曲线 (
( 为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移
为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移 个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线
个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线 .以坐标原点为极点,
.以坐标原点为极点, 的非负半轴为极轴,建立的极坐标中的曲线
的非负半轴为极轴,建立的极坐标中的曲线 的方程为
的方程为 ,求
,求 和
和 公共弦的长度.
公共弦的长度.
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:解答题
设直线 的参数方程为
的参数方程为 (t为参数),若以直角坐标系
(t为参数),若以直角坐标系 的
的 点为极点,
点为极点, 轴为极轴,选择相同的长度单位建立极坐标系,得曲线
轴为极轴,选择相同的长度单位建立极坐标系,得曲线 的极坐标方程为ρ=
的极坐标方程为ρ= .
.
(1)将曲线 的极坐标方程化为直角坐标方程,并指出曲线是什么曲线;
的极坐标方程化为直角坐标方程,并指出曲线是什么曲线;
(2)若直线 与曲线
与曲线 交于A、B两点,求
交于A、B两点,求 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(选修4-4:坐标系与参数方程) (本小题满分10分)
在直角坐标系xoy中,直线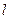 的参数方程为
的参数方程为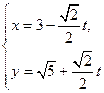 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为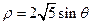 .
.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线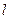 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为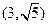 ,求|PA|+|PB|.
,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
((本小题满分10分)
选修4—4:坐标系与参数方程
已知直线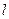 的参数方程为
的参数方程为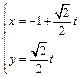 (
(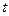 为参数),曲线C的极坐标方程是
为参数),曲线C的极坐标方程是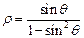 ,以极
,以极 点为原点,极轴为
点为原点,极轴为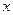 轴正方向建立直角坐标系,点
轴正方向建立直角坐标系,点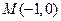 ,直线
,直线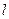 与曲线C交于A、B两点.
与曲线C交于A、B两点.
(1)写出直线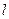 的极坐标方程与曲线C的普通方程;
的极坐标方程与曲线C的普通方程;
(2) 线段MA,MB长度分别记为|MA|,|MB|,求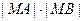 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本题有(1)、(2)、(3)三个选考题,每题7份,请考生任选2题作答,满分14分.
如果多做,则按所做的前两题计分.
选修4系列(本小题满分14分)
(1)(本小题满分7分)选修4-2:矩阵与变换
设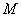 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到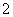 倍,纵坐标伸长到
倍,纵坐标伸长到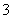 倍的伸压变换.
倍的伸压变换.
(Ⅰ)求矩阵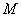 的特征值及相应的特征向量;
的特征值及相应的特征向量;
(Ⅱ)求逆矩阵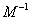 以及椭圆
以及椭圆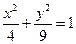 在
在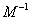 的作用下的新曲线的方程.
的作用下的新曲线的方程.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的极坐标方程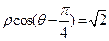 ,曲线C的参数方程为
,曲线C的参数方程为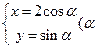 为参数),求曲线C截直线l所得的弦长
为参数),求曲线C截直线l所得的弦长
(3)(本小题满分7分)选修4—5:不等式选讲
已知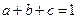 ,且
,且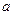 、
、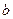 、
、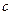 是正数,求证:
是正数,求证: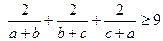 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图所示,PA、PB是⊙O的两条切线,A、B为切点,连接OP交AB于C,连接OA、OB,则图中等腰三角形、直角三角形的个数分别为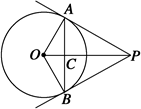
A.1,2 B.2,2 C.2,6 D.1,6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com