
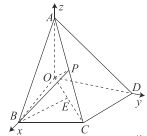
【题目】在如图(1)所示的四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .将
.将![]() 沿
沿![]() 折起,使二面角
折起,使二面角![]() 为直二面角(如图(2)),
为直二面角(如图(2)),![]() 为
为![]() 的中点.
的中点.
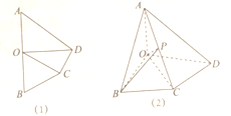
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由题意可得![]() 平面
平面![]() ,故
,故 ![]() . 以
. 以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示空间直角坐标系,明确平面BOP的法向量与AD的方向向量,利用二者共线,即可证得;
轴建立如图所示空间直角坐标系,明确平面BOP的法向量与AD的方向向量,利用二者共线,即可证得;
(2)求出平面![]() 的法向量,利用法向量的夹角余弦即可得到二面角
的法向量,利用法向量的夹角余弦即可得到二面角![]() 的余弦值.
的余弦值.
(1)证明:由题,知![]() ,
,![]() .
.
又∵二面角![]() 为直二面角,∴
为直二面角,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴
,∴![]() .
.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示空间直角坐标系.
轴建立如图所示空间直角坐标系.
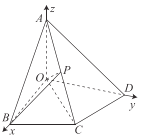
∵![]() ,
,![]() ,
,![]() ,
,
∴由平面几何知识,可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
设平面![]() 的法向量为
的法向量为![]() .
.
∴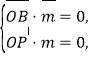 即
即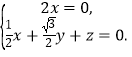
令![]() ,则
,则![]() .∴
.∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∴![]() 平面
平面![]() .
.
(2)解:设![]() 为
为![]() 中点,连接
中点,连接![]() ,如图.
,如图.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,交线为
,交线为![]() .
.
又∵![]() 为等边三角形,∴
为等边三角形,∴![]() .
.
又∵![]() 平面
平面![]() .∴
.∴![]() 平面
平面![]() .∴
.∴![]() 是平面
是平面![]() 的法向量.
的法向量.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若质地均匀的六面体玩具各面分别标有数字1,2,3,4,5,6.抛掷该玩具后,任何一个数字所在的面朝上的概率均相等.抛掷该玩具一次,记事件A=“向上的面标记的数字是完全平方数(即能写出整数的平方形式的数,如9=32,9是完全平方数)”
(1)甲、乙二人利用该玩具进行游戏,并规定:①甲抛掷一次,若事件A发生,则向上一面的点数的6倍为甲的得分;若事件A不发生,则甲得0分;②乙抛掷一次,将向上的一面对应的数字作为乙的得分。现甲、乙二人各抛掷该玩具一次,分别求二人得分的期望;
(2)抛掷该玩具一次,记事件B=“向上一面的点数不超过![]() ”,若事件A与B相互独立,试求出所有的整数
”,若事件A与B相互独立,试求出所有的整数![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某良种培育基地正在培育一种小麦新品种A,将其与原有的一个优良品种B进行对照试验,两种小麦各种植了24亩,所得亩产数据(单位:千克)如下:
品种A:357,359,367,368,375,388,392,399,400,405,412,414,415,421,423,423,427,430,430,434,443,445,451,454
品种B:363,371,374,383,385,386,391,392,394,395,397,397,400,401,401,403,406,407,410,412,415,416,422,430
(1)画出茎叶图.
(2)用茎叶图处理现有的数据,有什么优点?
(3)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() 是边长等于2的等边三角形,四边形
是边长等于2的等边三角形,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的点,
上的点,![]() .
.![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
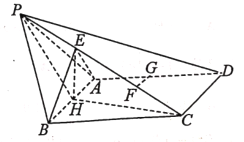
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com