
分析 (Ⅰ)由代入法可得直线l的普通方程;由ρ=$\sqrt{{x}^{2}+{y}^{2}}$可得曲线C的直角坐标方程,再由圆心到直线的距离公式判断d与r的关系,即可得到公共点的个数;
(Ⅱ)由题意可得曲线Ω的方程:$\left\{\begin{array}{l}x=cosθ\\ y=2sinθ\end{array}\right.(θ为参数)$,代入4x2+xy+y2,运用同角的平方关系和二倍角正弦公式,结合正弦函数的值域即可得到所求最大值及M的坐标.
解答 解:(Ⅰ)直线l的参数方程为$\left\{\begin{array}{l}x=\sqrt{2}+t\\ y=1-2t\end{array}$(t为参数方程),
即为直线l的方程为$2x+y=2\sqrt{2}+1$,由圆C的极坐标方程为ρ=1,
可得圆C的方程是x2+y2=1.
圆心(0,0)到直线l的距离为$d=\frac{{|{0-0-2\sqrt{2}-1}|}}{{\sqrt{4+1}}}>1$,
所以直线l与圆的公共点个数为0个.
(Ⅱ)圆C的参数方程是$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$(0≤θ<2π),
所以曲线Ω的方程:$\left\{\begin{array}{l}x=cosθ\\ y=2sinθ\end{array}\right.(θ为参数)$,
则4x2+xy+y2=4cos2θ+cosθ•2sinθ+4sin2θ=4+sin2θ,
所以$θ=\frac{π}{4}或θ=\frac{5π}{4}$时,4x2+xy+y2取得最大值5,
此时M的坐标为$(\frac{{\sqrt{2}}}{2},\sqrt{2})或(-\frac{{\sqrt{2}}}{2},-\sqrt{2})$.
点评 本题考查参数方程、极坐标方程和普通方程的互化,考查直线和圆的位置关系的判断,同时考查参数方程的运用和三角函数的恒等变换,以及正弦函数的值域,考查化简整理的运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
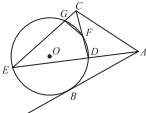 如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB.
如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
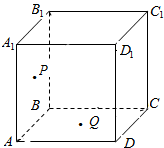 如图所示,已知P,Q是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.
如图所示,已知P,Q是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com