
分析 (Ⅰ)在已知二项式中分别取x=0、x=1联立求得a1+a2+a3+a4;
(Ⅱ)展开平方差公式,在已知二项式中分别取x=-1、x=1联立求${(a}_{0}{{+a}_{2}+a}_{4})^2-{(a}_{1}{+a}_{3})^{2}$;
(Ⅲ)结合(Ⅰ)、(Ⅱ)求得|a1|+|a2|+|a3|+|a4|.
解答 解:(Ⅰ)在(2x-3)4=${a}_{0}{+a}_{1}x{+a}_{2}{x}^{2}{+a}_{3}{x}^{3}{+a}_{4}{x}^{4}$中,
取x=0,得a0=81,取x=1,得a0+a1+a2+a3+a4=1,
∴a1+a2+a3+a4 =-80;
(Ⅱ)在(2x-3)4=${a}_{0}{+a}_{1}x{+a}_{2}{x}^{2}{+a}_{3}{x}^{3}{+a}_{4}{x}^{4}$中,
取x=1,得a0+a1+a2+a3+a4=1,
取x=-1,得a0-a1+a2-a3+a4=625,
∴${(a}_{0}{{+a}_{2}+a}_{4})^2-{(a}_{1}{+a}_{3})^{2}$
=(a0+a1+a2+a3+a4)(a0-a1+a2-a3+a4)=625;
(Ⅲ)由二项式可知,|a1|+|a2|+|a3|+|a4|=-a1+a2-a3+a4,
由(Ⅰ)知,a0=81,由(Ⅱ)知,a0-a1+a2-a3+a4=625,
∴|a1|+|a2|+|a3|+|a4|=-a1+a2-a3+a4=625-81=544.
点评 本题考查二项式系数的性质,考查了特值法的应用,是中档题.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
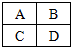 对如图中的A、B、C、D四个区域染色,每块区域染一种颜色,有公共边的区域不同色,现有红、黄、蓝三种不同颜色可以选择,则不同的染色方法共有( )
对如图中的A、B、C、D四个区域染色,每块区域染一种颜色,有公共边的区域不同色,现有红、黄、蓝三种不同颜色可以选择,则不同的染色方法共有( )| A. | 12种 | B. | 18种 | C. | 20种 | D. | 22种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin2α | B. | cos2α | C. | tan2α | D. | cot2α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,0)∪(1,+∞) | C. | (0,1) | D. | (-1,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}}}{8}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com