
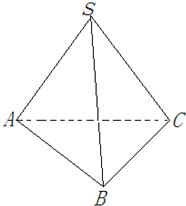
 如图所示,已知SA=AB=BC=1,以SC为斜边的Rt△SAC≌Rt△SBC,且$\overrightarrow{AC}•\overrightarrow{SB}=\frac{3}{4}$.
如图所示,已知SA=AB=BC=1,以SC为斜边的Rt△SAC≌Rt△SBC,且$\overrightarrow{AC}•\overrightarrow{SB}=\frac{3}{4}$.分析 (1)取M为SB的中点,连接AM,则AM⊥SB,又BC⊥SB,故利用向量$\overrightarrow{AM}$,$\overrightarrow{BC}$的夹角,利用余弦定理可求二面角A-SB-C的余弦值.
(2)异面直线AS,BC所成角转化为向量$\overrightarrow{AS}$,$\overrightarrow{BC}$的夹角问题,从而得解.
解答 解:(1)取M为SB的中点,连接AM,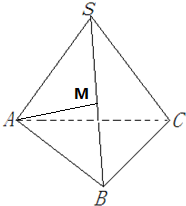
则AM⊥SB,
$\overrightarrow{AC}$=$\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{BC}$,
∴$\overrightarrow{AC}$•$\overrightarrow{SB}$=$\overrightarrow{AM}$•$\overrightarrow{SB}$+$\frac{1}{2}$$\overrightarrow{SB}$2+$\overrightarrow{BC}$•$\overrightarrow{SB}$=$\frac{1}{2}$$\overrightarrow{SB}$2=$\frac{3}{4}$
∴|$\overrightarrow{SB}$|=$\frac{\sqrt{6}}{2}$.
设二面角A-SB-C为α,
∵AC=SB=$\frac{\sqrt{6}}{2}$,AM=$\frac{\sqrt{10}}{4}$,BM=$\frac{\sqrt{6}}{4}$,BC=1
∴AC2=AM2+BC2+BM2-2AM•BC•cosα,
∴cosα=$\frac{\sqrt{10}}{10}$,
∴二面角A-SB-C的余弦值为$\frac{\sqrt{10}}{10}$.
(2)$\overrightarrow{AS}$=$\overrightarrow{AM}$-$\overrightarrow{SM}$=$\overrightarrow{AM}$,
∴$\overrightarrow{AS}$•$\overrightarrow{BC}$=$\overrightarrow{AM}$•$\overrightarrow{BC}$=-$\frac{1}{4}$,
∴异面直线AS,BC所成角所成角的余弦值为$\frac{1}{4}$.
点评 本题以向量为载体,考查面面角,线线角,关键是利用好向量条件.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 3 | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD的底面是菱形,对角线AC、BD交于点O,OA=3,OB=4,OP=6,OP⊥底面ABCD,点满足$\overrightarrow{PM}$=t$\overrightarrow{PC}$,t∈(0,1).
如图,已知四棱锥P-ABCD的底面是菱形,对角线AC、BD交于点O,OA=3,OB=4,OP=6,OP⊥底面ABCD,点满足$\overrightarrow{PM}$=t$\overrightarrow{PC}$,t∈(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
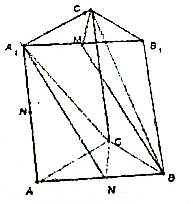 如图:直三棱柱ABC-A1B1C1,底面三角形ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,M、N分别为A1B1、AB的中点.
如图:直三棱柱ABC-A1B1C1,底面三角形ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,M、N分别为A1B1、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 7 | 14 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 17 | x | 4 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 4 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com