
分析 (Ⅰ)利用椭圆的方程,求出a,b,c.通过椭圆的定义求解三角形的周长,求解椭圆的离心率.
(Ⅱ)联立$\left\{{\begin{array}{l}{\sqrt{2}x-2y+m=0}\\{\frac{x^2}{4}+\frac{y^2}{2}=1}\end{array}}\right.$,利用直线l与椭圆C有两个交点,求出-4<m<0或0<m<4.设A(x1,y1),B(x2,y2),结合韦达定理,求解AB坐标,设直线PA与PB的斜率分别为k1,k2,推出k1+k2=0,即可证明|PM|=|PN|.
解答 解:(Ⅰ)由题意可知,a2=4,b2=2,所以c2=2.
因为$P(\sqrt{2},1)$是椭圆C上的点,由椭圆定义得|PF1|+|PF2|=4.
所以△PF1F2的周长为$4+2\sqrt{2}$.
易得椭圆的离心率$e=\frac{c}{a}=\frac{{\sqrt{2}}}{2}$.…(4分)
(Ⅱ)证明:由$\left\{{\begin{array}{l}{\sqrt{2}x-2y+m=0}\\{\frac{x^2}{4}+\frac{y^2}{2}=1}\end{array}}\right.$得$4{x^2}+2\sqrt{2}mx+{m^2}-8=0$.
因为直线l与椭圆C有两个交点,并注意到直线l不过点P,
所以$\left\{{\begin{array}{l}{8{m^2}-4×4({m^2}-8)>0}\\{m≠0}\end{array}}\right.$解得-4<m<0或0<m<4.
设A(x1,y1),B(x2,y2),则${x_1}+{x_2}=-\frac{{\sqrt{2}}}{2}m$,${x_1}{x_2}=\frac{{{m^2}-8}}{4}$,${y_1}=\frac{{\sqrt{2}{x_1}+m}}{2}$,${y_2}=\frac{{\sqrt{2}{x_2}+m}}{2}$.
显然直线PA与PB的斜率存在,设直线PA与PB的斜率分别为k1,k2,
则${k_1}+{k_2}=\frac{{{y_1}-1}}{{{x_1}-\sqrt{2}}}+\frac{{{y_2}-1}}{{{x_2}-\sqrt{2}}}$=$\frac{{(\frac{{\sqrt{2}{x_1}+m}}{2}-1)({x_2}-\sqrt{2})+(\frac{{\sqrt{2}{x_2}+m}}{2}-1)({x_1}-\sqrt{2})}}{{({x_1}-\sqrt{2})({x_2}-\sqrt{2})}}$
=$\frac{{(\sqrt{2}{x_1}+m-2)({x_2}-\sqrt{2})+(\sqrt{2}{x_2}+m-2)({x_1}-\sqrt{2})}}{{2({x_1}-\sqrt{2})({x_2}-\sqrt{2})}}$
=$\frac{{2\sqrt{2}{x_1}{x_2}+(m-4)({x_1}+{x_2})-2\sqrt{2}m+4\sqrt{2}}}{{2[{x_1}{x_2}-\sqrt{2}({x_1}+{x_2})+2]}}$
=$\frac{{\frac{{2\sqrt{2}({m^2}-8)}}{4}-\frac{{(m-4)2\sqrt{2}m}}{4}-\frac{{8\sqrt{2}m}}{4}+\frac{{16\sqrt{2}}}{4}}}{{2[{x_1}{x_2}-\sqrt{2}({x_1}+{x_2})+2]}}$
=$\frac{{2\sqrt{2}({m^2}-8)-(m-4)2\sqrt{2}m-8\sqrt{2}m+16\sqrt{2}}}{{8[{x_1}{x_2}-\sqrt{2}({x_1}+{x_2})+2]}}$
=$\frac{{2\sqrt{2}{m^2}-16\sqrt{2}-2\sqrt{2}{m^2}+8\sqrt{2}m-8\sqrt{2}m+16\sqrt{2}}}{{8[{x_1}{x_2}-\sqrt{2}({x_1}+{x_2})+2]}}=0$.
因为k1+k2=0,所以∠PMN=∠PNM.
所以|PM|=|PN|. …(14分)
点评 本题考查椭圆的简单性质以及直线与椭圆的位置关系的综合应用,考查分析问题解决问题的能力,转化思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
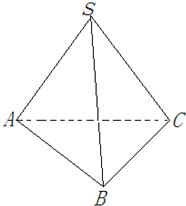 如图所示,已知SA=AB=BC=1,以SC为斜边的Rt△SAC≌Rt△SBC,且$\overrightarrow{AC}•\overrightarrow{SB}=\frac{3}{4}$.
如图所示,已知SA=AB=BC=1,以SC为斜边的Rt△SAC≌Rt△SBC,且$\overrightarrow{AC}•\overrightarrow{SB}=\frac{3}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 时刻 | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
| 水深(m) | 5.0 | 7.0 | 5.0 | 3.0 | 5.0 | 7.0 | 5.0 | 3.0 | 5.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | a=30 | b | |
| 捐款不超过500元 | c | d=6 | |
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 121 | B. | 122 | C. | 243 | D. | 244 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com