Question

16．已知抛物线y²=2px的焦点为F，若该抛物线上有一点A，满足直线FA的倾斜角为120°，且|FA|=4，
（1）求抛物线方程；
（2）若抛物线上另有两点B，C满足$\overrightarrow{FA}+\overrightarrow{FB}+\overrightarrow{FC}=\overrightarrow 0$，求直线BC的方程．

Answer 1

分析 （1）如图，设抛物线的准线为l，过A作AM⊥l，垂足为M．由|AF|=4可得|AM|=4，由∠AFx=120°，可知|NF|=|AM|+|AF|cos60°=6，由抛物线的定义即可得出．
（2）由（1）可知点$A（1，2\sqrt{3}）$，可设点B（x₁，y₁），C（x₂，y₂），由$\overrightarrow{FA}+\overrightarrow{FB}+\overrightarrow{FC}=\overrightarrow 0$，可得x₁+x₂=8，${y_1}+{y_2}=-2\sqrt{3}$，再利用中点坐标公式、斜率计算公式即可得出．

解答 解：（1）如图，设抛物线的准线为l，过A作AM⊥l，垂足为M．
由|AF|=4可得|AM|=4，由∠AFx=120°，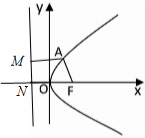
可知|NF|=|AM|+|AF|cos60°=6，由抛物线的定义可得p=|NF|=6，
即抛物线方程为y²=12x．
（2）由（1）可知点$A（1，2\sqrt{3}）$，可设点B（x₁，y₁），C（x₂，y₂），
由$\overrightarrow{FA}+\overrightarrow{FB}+\overrightarrow{FC}=\overrightarrow 0$，可得：$（-2，2\sqrt{3}）+（{x_1}-3，{y_1}）+（{x_2}-3，{y_2}）=（0，0）$，
即得x₁+x₂=8，${y_1}+{y_2}=-2\sqrt{3}$，
即BC中点坐标为$（4，-\sqrt{3}）$，
∵${y}_{1}^{2}=12{x}_{1}$，${y}_{2}^{2}$=12x₂，
∴${y}_{1}^{2}-{y}_{1}^{2}$=12（x₁-x₂），
而BC斜率$k=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{12}{{{y_1}+{y_2}}}=-2\sqrt{3}$，
∴直线BC方程为：$y+\sqrt{3}=-2\sqrt{3}（x-4）$，
整理为：$2\sqrt{3}x+y-7\sqrt{3}=0$，

点评 本题考查了抛物线的定义、中点坐标公式、斜率计算公式、点与抛物线的关系、向量坐标运算，考查了推理能力与计算能力，属于中档题．