
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{15}}}{4}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 求出椭圆的焦点坐标,利用|AB|=1,求出a、b、c,然后求解离心率即可.
解答 解:焦点在x轴的椭圆方程:$\frac{x^2}{a^2}+{y^2}=1$,焦点坐标(±$\sqrt{{a}^{2}-1}$,0),不妨A($\sqrt{{a}^{2}-1}$,$\frac{1}{2}$),
可得$\frac{{a}^{2}-1}{{a}^{2}}+\frac{1}{4}=1$,解得a=2,
椭圆的离心率为:e=$\frac{\sqrt{{a}^{2}-1}}{a}$=$\frac{\sqrt{3}}{2}$.
故选:A.
点评 本题考查椭圆的简单性质,离心率的求法,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | $\frac{32π}{3}$ | C. | $\frac{20\sqrt{5}π}{3}$ | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
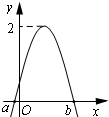 如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )
如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=5cosx | B. | y=5cos4x | C. | y=-5cosx | D. | y=-5 cos4x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线y2=2px的焦点为F,若该抛物线上有一点A,满足直线FA的倾斜角为120°,且|FA|=4,
已知抛物线y2=2px的焦点为F,若该抛物线上有一点A,满足直线FA的倾斜角为120°,且|FA|=4,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y | 3 | m | 7 | 10 |
| A. | 1 | B. | $\frac{3}{2}$ | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com