
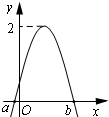
 如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )
如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
分析 由最大值求出A,结合图象可得a+b=x1 +x2 .由五点法作图求得a+b=$\frac{π}{2}$-φ,由f(a+b)=2sinφ=$f({x_1}+{x_2})=\sqrt{3}$,可得sinφ的值,从而求得φ的值.
解答 解:根据函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,可得A=2,周期为$\frac{2π}{2}$=π,∴b-a=$\frac{π}{2}$.
由f(x1)=f(x2),可得函数的图象关于直线x=$\frac{{x}_{1}{+x}_{2}}{2}$=$\frac{a+b}{2}$对称,故a+b=x1 +x2 .
由五点法作图可得2a+φ=0,2b+φ=π,∴a+b=$\frac{π}{2}$-φ.
结合f(a+b)=f($\frac{π}{2}$-φ)=2sin(π-2φ+φ)=2sinφ=$f({x_1}+{x_2})=\sqrt{3}$,可得sinφ=$\frac{\sqrt{3}}{2}$,∴φ=$\frac{π}{3}$,
故选:D.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象特征,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{11}{3}$ | B. | -17 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解某校高三毕业生报考体育专业学生的体重(单位:千克),将他们的体重数据整理后得到如下频率分布直方图.已知图中从左到右前3个小组的频率之比为1:2:3,其中第二小组的频数为12.
为了解某校高三毕业生报考体育专业学生的体重(单位:千克),将他们的体重数据整理后得到如下频率分布直方图.已知图中从左到右前3个小组的频率之比为1:2:3,其中第二小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{15}}}{4}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 15 | C. | 18 | D. | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com