
分析 (1)平方得x2=2cos2α$+2\sqrt{3}sinαcosα+1$,代入第二个式子化简得出ρsinθ+ρcosθ=t,根据y=ρsinθ,x=ρcosθ,化简得出x+y=t.
(2)t=5,并且向左下方平行运动直到相切之前总有公共点,相切时仍只有一个公共点,联立$\left\{\begin{array}{l}{x+y=t}\\{y={x}^{2}-1}\end{array}\right.$利用判别式问题求解.
解答 解:(1)由x=$\sqrt{3}cosα+sinα$,得x2=2cos2α$+2\sqrt{3}sinαcosα+1$,
所以曲线M可化为y=x2-1,x∈[-2,2],由ρsin($θ+\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$t,
得$\frac{\sqrt{2}}{2}$ρsinθ$+\frac{\sqrt{2}}{2}$ρcosθ=$\frac{\sqrt{2}}{2}$t,
所以ρsinθ+ρcosθ=t,
所以N可化为x+y=t,
(2)若曲线N与曲线M有公共点,则当直线N过点(2,3)时,满足要求,
此时t=5,并且向左下方平行运动直到相切之前总有公共点,相切时仍只有一个公共点,
联立$\left\{\begin{array}{l}{x+y=t}\\{y={x}^{2}-1}\end{array}\right.$得x2+x-1-t=0,
△=1+4(1+t)=0,解得t=$-\frac{5}{4}$,综上可得t的取值范围$-\frac{5}{4}$≤t≤5.
点评 本题考查了参数方程的与普通方程的转化问题,曲线的公共点问题,利用方程有解问题,转化为判别式求解,思路简单,属于中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | $\frac{32π}{3}$ | C. | $\frac{20\sqrt{5}π}{3}$ | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
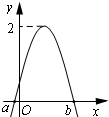 如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )
如图是函数$f(x)=Asin(2x+φ)(A>0,|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则φ的值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com