
分析 原题要求利用数学归纳法证明数列不等式,首先验证n=2时不等式成立,然后假设n=k时不等式成立,然后利用归纳假设证明n=k+1时不等式成立,最后下结论.
解答 证明:①当n=2时,原不等式左边=1+$\frac{1}{{2}^{2}}$=$\frac{5}{4}$,右边=2-$\frac{1}{2}$=$\frac{3}{2}$,左边<右边,不等式成立;
②假设当n=k时,原不等式成立,即1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{k}^{2}}$<2-$\frac{1}{k}$成立,
则当n=k+1时,1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{k}^{2}}$+$\frac{1}{(1+k)^{2}}$<2-$\frac{1}{k}$+$\frac{1}{(1+k)^{2}}$=2-$\frac{{k}^{2}+2k+1-k}{k(k+1)^{2}}$,
=2-$\frac{{k}^{2}+k+1}{k(k+1)^{2}}$=2-$\frac{k(k+1)}{k(k+1)^{2}}$-$\frac{1}{k(k+1)^{2}}$<2-$\frac{k(k+1)}{k(k+1)^{2}}$=2-$\frac{1}{k+1}$,
即n=k+1时原不等式也成立.
综上,对于任意n(n∈N*且n≥2)原不等式成立.
点评 本题考查利用数学归纳法证明数列不等式,利用归纳法证明与自然数有关的命题,关键是用上归纳假设,是中档题.


科目:高中数学 来源:2016-2017学年江西省高一上学期第一次月考数学试卷(解析版) 题型:解答题
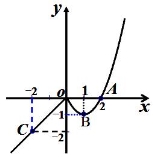
如图是函数f(x)的图象,OC段是射线,而OBA是抛物线的一部分,试写出f(x)的函数表达式.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,C.已知3cos(B-C)-1=6cosBcosC.
(1)求cosA;
(2)若a=3,△ABC的面积为2 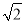 ,求b,C.
,求b,C.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
某企业有职工150人,其中高级职工15人,中级职工45人,一般职工90人,现抽30人进行分层抽样,则各职称人数分别为( )
A.5,10,15 B.3,9,18
C.3,10,17 D.5,9,16
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
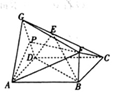 如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC上除两端点外的一点.
如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC上除两端点外的一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $k>-\frac{5}{6}$ | B. | $k<-\frac{5}{6}$ | C. | $k<-\frac{3}{4}$ | D. | $k>-\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com