
 如图所示,已知AB为圆O的直径,C,D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG.
如图所示,已知AB为圆O的直径,C,D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG.分析 (I)要证明C是劣弧BD的中点,即证明弧BC与弧CD相等,即证明∠CAB=∠DAC,根据已知中CF=FG,AB是圆O的直径,CE⊥AB于E,我们易根据同角的余角相等,得到结论.
(II)由已知及(I)的结论,我们易证明△BFC及△GFC均为等腰三角形,即CF=BF,CF=GF,进而得到结论.
解答 解:(I)∵CF=FG
∴∠CGF=∠FCG
∴AB圆O的直径
∴∠ACB=∠ADB=90°
∵CE⊥AB
∴∠CEA=90°
∵∠CBA=90°-∠CAB,∠ACE=90°-∠CAB
∴∠CBA=∠ACE
∵∠CGF=∠DGA,
∴∠DGA=∠ABC
∴∴∠CAB=∠DAC
∴C为劣弧BD的中点,
∴AC是∠DAB的平分线;
(II)∵∠GBC=90°-∠CGB,∠FCB=90°-∠GCF
∴∠GBC=∠FCB
∴CF=FB
同理可证:CF=GF
∴BF=FG,
∵OA=OB,
∴OF∥AG.
点评 本题考查的知识点圆周角定理及其推理,同(等)角的余角相等,其中根据AB是圆O的直径,CE⊥AB于E,找出要证明相等的角所在的直角三角形,是解答本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2},\frac{2}{3}}]$ | B. | $({\frac{2}{3},\frac{3}{4}}]$ | C. | $({\frac{3}{4},\frac{4}{5}}]$ | D. | $({\frac{4}{5},\frac{5}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 120° | C. | 60°或120° | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
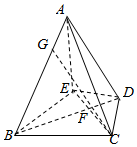 如图所示,在四棱锥A-BCDE中,AE⊥平面BCDE,△BCE为正三角形,BD和CE的交点F,恰好平分CE,AE=BE=2,∠CDE=120°,AC=$\frac{\sqrt{2}}{2}$.
如图所示,在四棱锥A-BCDE中,AE⊥平面BCDE,△BCE为正三角形,BD和CE的交点F,恰好平分CE,AE=BE=2,∠CDE=120°,AC=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 9$\sqrt{3}$ | B. | 9$\sqrt{2}$+$\frac{9\sqrt{3}}{4}$ | C. | 12$\sqrt{2}$ | D. | 12$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,以△ABC的BC边为直径的半圆交AB于点D,交AC于点E,EF⊥BC于F,BF:FC=5:1,AB=8,AE=2,则AD长为( )
如图,以△ABC的BC边为直径的半圆交AB于点D,交AC于点E,EF⊥BC于F,BF:FC=5:1,AB=8,AE=2,则AD长为( )| A. | $\frac{{1+\sqrt{21}}}{2}$ | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{{1+\sqrt{2}}}{2}$ | D. | $\frac{43}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
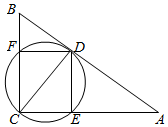 如图,在三角形ABC中,∠ACB=90°,CD⊥AB于D,以CD为直径的圆分别交AC、BC于E、F.
如图,在三角形ABC中,∠ACB=90°,CD⊥AB于D,以CD为直径的圆分别交AC、BC于E、F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|x<0} | C. | {x|x<-1或0<x<1} | D. | {x|x<-1或x>1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com