
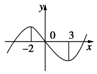
 函数f(x)=x3+bx2+cx+d的图象如图,则函数g(x)=log${\;}_{\frac{1}{3}}$(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递增区间为( )
函数f(x)=x3+bx2+cx+d的图象如图,则函数g(x)=log${\;}_{\frac{1}{3}}$(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递增区间为( )| A. | [-2,+∞) | B. | (-∞,-2) | C. | (3,+∞) | D. | [3,+∞) |
分析 根据函数的图象,结合函数极值和导数的关系求出b,c,d的值,利用换元法结合复合函数单调性之间的关系进行转化求解即可.
解答 解:由图象得函数过原点,则f(0)=d=0,
函数的导数f′(x)=3x2+2bx+c,
x=-2和x=3是函数f(x)的极值点,
则x=-2和x=3是方程f′(x)=3x2+2bx+c=0的两个根,
则$\left\{\begin{array}{l}{-2+3=-\frac{2b}{3}}\\{-2×3=\frac{c}{3}}\end{array}\right.$,即b=-$\frac{3}{2}$,c=-18,
则g(x)=log${\;}_{\frac{1}{3}}$(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)=log${\;}_{\frac{1}{3}}$(x2-x-6),
设t=x2-x-6,则函数y=log${\;}_{\frac{1}{3}}$t为减函数,
由t=x2-x-6>0得x>3或x<-2,
要求g(x)的单调递增区间,即求函数t=x2-x-6的单调递减区间,
∵t=x2-x-6的单调递减区间为(-∞,-2),
∴函数g(x)=log${\;}_{\frac{1}{3}}$(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递增区间为(-∞,-2),
故选:B
点评 本题主要考查函数单调性的求解,利用复合函数单调性的关系以及函数极值和导数的关系求出未知数是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{2}$] | B. | (0,1] | C. | [-$\frac{1}{2}$,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=|x| | B. | y=3-x | C. | y=$\frac{1}{x}$ | D. | y=-x2+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(文)试卷(解析版) 题型:选择题
甲、乙两名篮球运动员近几场比赛得分统计成茎叶图如图,甲,乙两人的平均数与中位数分别相等,则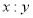 为( )
为( )

A.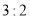 B.
B.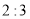 C.
C.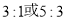 D.
D.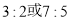
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com