
分析 (Ⅰ)由α的范围和平方关系求出sinα,再由两角和的正弦函数求出sin(α+$\frac{π}{6}$)的值;
(Ⅱ)由α,β为锐角得α+β∈(0,π),由平方关系求出sin(α+β),再由两角差的余弦函数求出cosβ=cos[(α+β)-α]的值.
解答 解:(Ⅰ)∵α为锐角,sinα=$\frac{1}{7}$,
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{4\sqrt{3}}{7}$,
∴sin(α+$\frac{π}{6}$)=sinαcos$\frac{π}{6}$+cosαsin$\frac{π}{6}$)
=$\frac{1}{7}×\frac{\sqrt{3}}{2}+\frac{4\sqrt{3}}{7}×\frac{1}{2}$=$\frac{5\sqrt{3}}{14}$;
(Ⅱ)∵α,β为锐角,∴α+β∈(0,π),
由cos(α+β)=$\frac{3}{5}$得,sin(α+β)=$\sqrt{1-{cos}^{2}(α+β)}$=$\frac{4}{5}$,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=$\frac{3}{5}×\frac{4\sqrt{3}}{7}+\frac{4}{5}×\frac{1}{7}$=$\frac{4+12\sqrt{3}}{35}$.
点评 本题考查由两角和与差的正弦、余弦函数,以及平方关系的应用,注意角的范围和角之间的关系,属于中档题.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{4}{π}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 若函数f(x)=Asin(ωx+φ)的部分图象如图所示:
若函数f(x)=Asin(ωx+φ)的部分图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 通过市场调查,得到某产品的资金投入x(万元)与获得的利润y(万元)的数据,如表所示:
通过市场调查,得到某产品的资金投入x(万元)与获得的利润y(万元)的数据,如表所示:| 资金投入 x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 7 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<3} | B. | {x|0<x<3} | C. | {x|x>-1} | D. | {x|x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
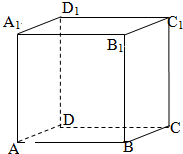 ABCD-A1B1C1D1是单位正方体,黑白两只蚂蚁从点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.白蚂蚁爬行的路线是AA1→A1D1,…,黑蚂蚁爬行的路线是AB→BB1,…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(i∈N*),设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处,则此时黑白蚂蚁的距离是( )
ABCD-A1B1C1D1是单位正方体,黑白两只蚂蚁从点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.白蚂蚁爬行的路线是AA1→A1D1,…,黑蚂蚁爬行的路线是AB→BB1,…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(i∈N*),设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处,则此时黑白蚂蚁的距离是( )| A. | $\sqrt{2}$ | B. | 1 | C. | 0 | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com