Question

直线y=a与函数f(x)=x³-3x的图象有相异的三个交点，求a的取值范围.

Answer 1

分析：∵y=a与f(x)=x³-3x的图象有相异的三个交点,知f(x)=x³-3x有两个“拐点”(已具备),且两“拐点”分布在y=a的两侧,即有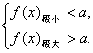故需求f(x)的极值.

解：研究函数y=a与函数f(x)=x³-3x的交点个数，由于y=a是一条平行于x轴(a=0时与x轴重合)的直线，

∴只需研究函数f(x)=x³-3x图象的变化趋势即可.

∵f′(x)=3x²-3=3(x-1)(x+1),∴在区间(-∞,-1]上,f(x)递增；

    在［-1,1］上,f(x)递减；

    在［1,+∞)上,f(x)递增.

∴［f(x)］_极小值=-2，［f(x)］_极大值=2.

    因此，要使y=a与函数f(x)的图象有相异的三个交点，必须有a∈(-2,2).