
已知点F(1,0),⊙F与直线4x+3y+1=0相切,动圆M与⊙F及y轴都相切.
(1)求点M的轨迹C的方程;
(2)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向⊙F各引一条切线,切点分别为P,Q,记α=∠PAF,β=∠QBF,求证sinα+sinβ是定值.
(1)⊙F的半径为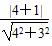 =1,⊙F的方程为(x-1)2+y2=1.
=1,⊙F的方程为(x-1)2+y2=1.
由题意动圆M与⊙F及y轴都相切,分以下情况:
①动圆M与⊙F及y轴都相切,但切点不是原点的情况.
作MH⊥y轴于H,则|MF|-1=|MH|,即|MF|=|MH|+1,则|MF|=|MN|(N是过M作直线x=-1的垂线的垂足),则点M的轨迹是以F为焦点,x=-1为准线的抛物线.
∴点M的轨迹C的方程为y2=4x(x≠0).
②动圆M与⊙F及y轴都相切且切于原点的情况.
此时点M的轨迹C的方程为y=0(x≠0,1).
(2)由于直线l过点F与C交于A、B两点,且F不尽在C上,∴l只能与y2=4x(x≠0)交于两点.
当l不与x轴垂直时,直线l的方程为y=k(x-1),
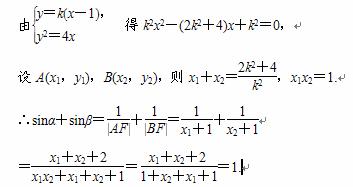 当l与x轴垂直时,也可得sinα+sinβ=1.
当l与x轴垂直时,也可得sinα+sinβ=1.
综上,有sinα+sinβ=1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知动圆过定点A(4,0),且在y轴上截得弦长MN的长为8.
(1)求动圆圆心的轨迹C的方程;
(2)已知点B(-1,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l1:4x-3y+6=0和直线l2:x=-1,P是抛物线y2=4x上一动点,则点P到直线l1和直线l2的距离之和的最小值是( )
A.2 B.3
C.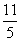 D.
D.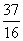
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线y2=2px(p>0),过其焦点且斜率为1的直线交抛物线于A、B两点,若线段AB的中点的纵坐标为2,则该抛物线的准线方程为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
设曲线x2-y2=0与抛物线y2=-4x的准线围成的三角形区域(包含边界)为D,P(x,y)为D内的一个动点,则目标函数z=x-2y+5的最大值为( )
A.4 B.5
C.8 D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com