
分析 (Ⅰ)由正弦定理,两角和的正弦函数公式化简已知等式可得2sinBcosC=sinB,结合sinB≠0,可求cosC=$\frac{1}{2}$,又C为三角形内角,即可得解C的值.
(Ⅱ)由已知及余弦定理可得AC2-$\sqrt{2}$AC-24=0,解得AC,进而在△ABC中,由余弦定理,可求AB的值.
解答 (本题满分为12分)
解:(Ⅰ)因为$\frac{2b-a}{cosA}=\frac{c}{cosC}$,
所以,由正弦定理,得$\frac{2sinB-sinA}{cosA}$=$\frac{sinC}{cosC}$,…(2分)
即2sinBcosC=sinAcosC+cosAsinC=sinB,
因为sinB≠0,
所以cosC=$\frac{1}{2}$,…(5分)
因为C为三角形内角,
所以C=$\frac{π}{3}$.…(6分)
(Ⅱ)在△AMC中,CM=$\sqrt{2}$,AM=$\sqrt{26}$,C=$\frac{π}{3}$,
由余弦定理,得26=AC2+2-2×$\sqrt{2}$ACcos$\frac{π}{3}$,
即AC2-$\sqrt{2}$AC-24=0,…(8分)
解得AC=4$\sqrt{2}$(舍去AC=-3$\sqrt{2}$),…(10分)
在△ABC中,由余弦定理,得AB2=(4$\sqrt{2}$)2+(2$\sqrt{2}$)2-2×$4\sqrt{2}×2\sqrt{2}$cos$\frac{π}{3}$=24,
所以AB=2$\sqrt{6}$. …(12分)
点评 本题主要考查了正弦定理,两角和的正弦函数公式,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (1,+∞) | C. | [1,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
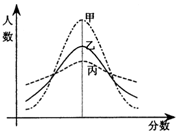 某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )
某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )| A. | 甲、乙、丙的总体的平均数不相同 | B. | 乙科总体的标准差及平均数都居中 | ||
| C. | 丙科总体的平均数最小 | D. | 甲科总体的标准差最小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 2 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com