练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知曲线y=$\frac{{x}^{2}}{2}$-3lnx的一条切线的与直线x+2y+10=0垂直，则切点的横坐标为（　　）
    A．$\frac{1}{3}$B．2C．1D．3

    分析 设出切点坐标，求出原函数的导函数，结合切线与直线x+2y+10=0垂直，可得关于切点横坐标的方程，求解得答案．

    解答 解：设切点坐标为（x0，y0），且x0＞0，
    由y′=x-$\frac{3}{x}$，得k=x0-$\frac{3}{{x}_{0}}$，
    ∵切线与直线x+2y+10=0垂直，
    ∴x0-$\frac{3}{{x}_{0}}$=2，解得x0=3或x0=-1（舍）．
    故选：D．

    点评 本题考查利用导数研究过曲线上某点处的切线方程，关键是明确函数在某点处的切线的斜率，就是函数在该点处的导数值，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

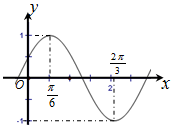    3．已知函数f（x）=Asin（ωx+φ）（A＞0，?＞0，|φ|＜$\frac{π}{2}$）的简图如下，则A，ω，φ分别为（　　）
    A．1，2，-$\frac{π}{3}$B．1，$\frac{1}{2}$，-$\frac{π}{3}$C．1，2，$\frac{π}{6}$D．1，$\frac{1}{2}$，$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在△ABC中，角A、B、C的对边分别为a、b、c，且$\frac{2b-a}{cosA}=\frac{c}{cosC}$．
    （Ⅰ）求角C的值；
    （Ⅱ）若BC=2$\sqrt{2}$，BC边上的中线AM=$\sqrt{26}$，求AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知方程$\frac{x^2}{m-1}+\frac{y^2}{4-m}=1$表示焦点在x轴上的双曲线的一个充分不必要条件是（　　）
    A．（4，+∞）B．（5，+∞）C．$（1，\frac{5}{2}）$D．（1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．若变量x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+y≤8\\ 2y-x≤4\end{array}\right.$，且z=5y-x的最大值为a，最小值为b，则a-b的值是（　　）
    A．16B．24C．30D．48

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．（1）椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点A（0，-1），且离心率为$\frac{\sqrt{2}}{2}$，求椭圆E的方程；
    （2）求经过M（2，$\sqrt{2}$），N（$\sqrt{6}$，1）两点的椭圆的标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知两点A（1，2）．B（2，1）在直线mx-y+1=0的异侧，则实数m的取值范围为（　　）
    A．（-∞，0）B．（1，+∞）C．（0，1）D．（-∞，0）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．为了考察某种药物预防禽流感的效果，某研究中心选了50只鸭子做实验，统计结果如下：
    得禽流感不得禽流感总计
    服药52025
    不服药151025
    总计203050
    （1）能有多大的把握认为药物有效？
    （2）在服药后得禽流感的鸭子中，有2只母鸭，3只公鸭，在这5只中随机抽取3只再进行研究，求至少抽到1只母鸭的概率．
    参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
    临界值表：
     P（K2≥k0） 0.10 0.05 0.01
     k0 2.706 3.841 6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．设$a，b，c∈（{0，\frac{π}{2}}）$，且满足cosa=a，sin（cosb）=b，cos（sinc）=c，则a，b，c的大小关系为b＜a＜c．

    查看答案和解析>>

    同步练习册答案