
| 得禽流感 | 不得禽流感 | 总计 | |
| 服药 | 5 | 20 | 25 |
| 不服药 | 15 | 10 | 25 |
| 总计 | 20 | 30 | 50 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
分析 (1)根据公式假设K2的值,对照临界值表即可得出结论;
(2)利用列举法求出基本事件数,计算所求的概率值.
解答 解:(1)假设H0:服药与家禽得流感没有关系,
则K2=$\frac{50{×(5×10-15×20)}^{2}}{20×30×25×25}$≈8.333>6.635
∵P(K2>6.635)=0.01,
1-0.01=0.99,
∴有99%的把握认为药物有效;
(2)记2只母鸭为a、b,3只公鸭为A、B、C,
则从这5只中随机抽取3只的基本事件为:
abA、abB、abC、aAB、aAC、aBC、bAB、bAC、bBC、ABC共10种,
则至少抽到1只母鸭的基本事件是9种,
故所求的概率为P=$\frac{9}{10}$.
点评 本题考查了独立性检验与列举法求古典概型的概率问题,是基础题目.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (1,+∞) | C. | [1,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 2 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | $({0,\frac{1}{2}}]$ | C. | $[{\frac{1}{2},2}]$ | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
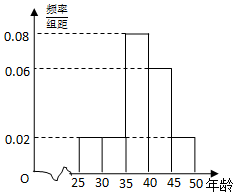 某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图:| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 | a | 150 | b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com