
【题目】已知a,b,c,使等式![]() N+都成立,
N+都成立,
(1)猜测a,b,c的值;(2)用数学归纳法证明你的结论。
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
先假设存在符合题意的常数a,b,c,再令n=1,n=2,n=3构造三个方程求出a,b,c,再用用数学归纳法证明成立,证明时先证:(1)当n=1时成立.(2)再假设n=k(k≥1)时,成立,即122+232+…+k(k+1)2=![]() (3k2+11k+10),再递推到n=k+1时,成立即可.
(3k2+11k+10),再递推到n=k+1时,成立即可.
(1):假设存在符合题意的常数a,b,c,
在等式122+232+…+n(n+1)2
=![]() (an2+bn+c)中,
(an2+bn+c)中,
令n=1,得4=![]() (a+b+c)①
(a+b+c)①
令n=2,得22=![]() (4a+2b+c)②
(4a+2b+c)②
令n=3,得70=9a+3b+c③
由①②③解得a=3,b=11,c=10,
于是,对于n=1,2,3都有
122+232+…+n(n+1)2=![]() (3n2+11n+10)(*)成立.
(3n2+11n+10)(*)成立.
(2)下面用数学归纳法证明:对于一切正整数n,(*)式都成立.
(1)当n=1时,由上述知,(*)成立.
(2)假设n=k(k≥1)时,(*)成立,
即122+232+…+k(k+1)2
=![]() (3k2+11k+10),
(3k2+11k+10),
那么当n=k+1时,
122+232+…+k(k+1)2+(k+1)(k+2)2
=![]() (3k2+11k+10)+(k+1)(k+2)2
(3k2+11k+10)+(k+1)(k+2)2
=![]() (3k2+5k+12k+24)
(3k2+5k+12k+24)
=![]() [3(k+1)2+11(k+1)+10],
[3(k+1)2+11(k+1)+10],
由此可知,当n=k+1时,(*)式也成立.
综上所述,当a=3,b=11,c=10时题设的等式对于一切正整数n都成立.


科目:高中数学 来源: 题型:
【题目】王老师的班上有四个体育健将甲、乙、丙、丁,他们都特别擅长短跑,在某次运动会上,他们四人要组成一个![]() 米接力队,王老师要安排他们四个人的出场顺序,以下是他们四人的对话:
米接力队,王老师要安排他们四个人的出场顺序,以下是他们四人的对话:
甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;
丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒;
王老师听了他们四人的对话,安排了一种合理的出场顺序,满足了他们的所有要求, 据此我们可以断定,在王老师安排的出场顺序中,跑第三棒的人是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是 . (写出所有正确说法的序号)
①若p是q的充分不必要条件,则p是q的必要不充分条件;
②命题“x∈R,x2+1>3x”的否定是“x∈R,x2+1<3x”;
③设x,y∈R.命题“若xy=0,则x2+y2=0”的否命题是真命题;
④若 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1底面是边长为1的正方形,高AA1= ![]() ,点A是平面α内的一个定点,AA1与α所成角为
,点A是平面α内的一个定点,AA1与α所成角为 ![]() ,点C1在平面α内的射影为P,当四棱柱ABCD﹣A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积= .
,点C1在平面α内的射影为P,当四棱柱ABCD﹣A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项都大于1,且a1=2,a ![]() ﹣an+1﹣a
﹣an+1﹣a ![]() +1=0(n∈N*).
+1=0(n∈N*).
(1)求证: ![]() ≤an<an+1≤n+2;
≤an<an+1≤n+2;
(2)求证: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <1.
<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了了解某地区电视观众对某类体育节目的收视情况随机抽取了100名观众进行调查,其中女性有55名.如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
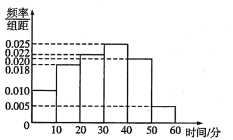
(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否认为“体育迷”与性别有关?
列联表,并据此资料你是否认为“体育迷”与性别有关?
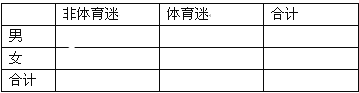
(2)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项都大于1,且a1=2,a ![]() ﹣an+1﹣a
﹣an+1﹣a ![]() +1=0(n∈N*).
+1=0(n∈N*).
(1)求证: ![]() ≤an<an+1≤n+2;
≤an<an+1≤n+2;
(2)求证: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <1.
<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知存在常数![]() ,那么函数
,那么函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,再由函数的奇偶性可知在
上是增函数,再由函数的奇偶性可知在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(1)判断函数![]() 的单调性,并证明:
的单调性,并证明:
(2)将前述的函数![]() 和
和![]() 推广为更为一般形式的函数
推广为更为一般形式的函数![]() ,使
,使![]() 和
和![]() 都是
都是![]() 的特例,研究
的特例,研究![]() 的单调性(只须归纳出结论,不必推理证明)
的单调性(只须归纳出结论,不必推理证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com