
【题目】过点![]() 斜率为正的直线交椭圆
斜率为正的直线交椭圆![]() 于
于![]() ,
,![]() 两点.
两点.![]() ,
,![]() 是椭圆上相异的两点,满足
是椭圆上相异的两点,满足![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() .则
.则![]() 外接圆半径的最小值为( )
外接圆半径的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
分析可知,P,C,D在一个阿波罗尼斯圆上,设其半径为r,且![]() ,分直线AB斜率存在及不存在两种情况分别讨论得解.
,分直线AB斜率存在及不存在两种情况分别讨论得解.
如图,
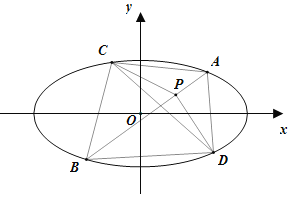
先固定直线AB,设![]() ,则
,则![]() ,其中
,其中![]() 为定值,
为定值,
故点P,C,D在一个阿波罗尼斯圆上,且![]() 外接圆就是这个阿波罗尼斯圆,设其半径为r,阿波罗尼斯圆会把点A,B其一包含进去,这取决于BP与AP谁更大,不妨先考虑
外接圆就是这个阿波罗尼斯圆,设其半径为r,阿波罗尼斯圆会把点A,B其一包含进去,这取决于BP与AP谁更大,不妨先考虑![]() 的阿波罗尼斯圆的情况,BA的延长线与圆交于点Q,PQ即为该圆的直径,如图:
的阿波罗尼斯圆的情况,BA的延长线与圆交于点Q,PQ即为该圆的直径,如图:
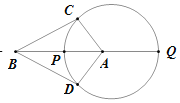
接下来寻求半径的表达式,
由![]() ,解得
,解得![]() ,
,
同理,当![]() 时有,
时有,![]() ,
,
综上,![]() ;
;
当直线AB无斜率时,与椭圆交点纵坐标为![]() ,则
,则![]() ;
;
当直线AB斜率存在时,设直线AB的方程为![]() ,即
,即![]() ,
,
与椭圆方程联立可得![]() ,
,
设![]() ,
,![]() ,则由根与系数的关系有,
,则由根与系数的关系有,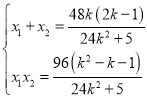 ,
,
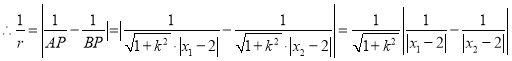 ,
,
注意到![]() 与
与![]() 异号,故
异号,故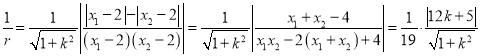 ,
,
设![]() ,则
,则 ,,当
,,当![]() ,即
,即![]() ,此时
,此时![]() ,故
,故![]() ,
,
又![]() ,综上外接圆半径的最小值为
,综上外接圆半径的最小值为![]() .
.
故选:D.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】迈入2018年后,直播答题突然就火了.在1月6号的一场活动中,最终仅有23人平分100万,这23人可以说是“学霸”级的大神.随着直播答题的发展,平台“烧钱大战”模式的可持续性受到了质疑,某网站随机选取1000名网民进行了调查,得到的数据如下表:
男 | 女 | |
认为直播答题模式可持续 | 360 | 280 |
认为直播答题模式不可持续 | 240 | 120 |
(1)根据表格中的数据,能否在犯错误不超过![]() 的前提下,认为对直播答题模式的态度与性别有关系?
的前提下,认为对直播答题模式的态度与性别有关系?
(2)已知在参与调查的1000人中,有20%曾参加答题游戏瓜分过奖金,而男性被调查者有15%曾参加游戏瓜分过奖金,求女性被调查者参与游戏瓜分过奖金的概率.
参考公式: ![]() .
.
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数组![]() ,
,![]() ,
,![]()
![]() ,数
,数![]() 称为数组
称为数组![]() 的元素.对于数组
的元素.对于数组![]() ,规定:
,规定:
①数组![]() 中所有元素的和为
中所有元素的和为![]() ;
;
②变换![]() ,
,![]() 将数组
将数组![]() 变换成数组
变换成数组![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数;
的最大整数;
③若数组![]() ,则当且仅当
,则当且仅当![]()
![]() 时,
时,![]() .
.
如果对数组![]() 中任意
中任意![]() 个元素,存在一种分法,可将其分为两组,每组
个元素,存在一种分法,可将其分为两组,每组![]() 个元素,使得两组所有元素的和相等,则称数组
个元素,使得两组所有元素的和相等,则称数组![]() 具有性质
具有性质![]() .
.
(Ⅰ)已知数组![]() ,
,![]() ,计算
,计算![]() ,
,![]() ,并写出数组
,并写出数组![]() 是否具有性质
是否具有性质![]() ;
;
(Ⅱ)已知数组![]() 具有性质
具有性质![]() ,证明:
,证明:![]() 也具有性质
也具有性质![]() ;
;
(Ⅲ)证明:数组![]() 具有性质
具有性质![]() 的充要条件是
的充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜率为![]() 的直线
的直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)设点![]() 在第一象限,过
在第一象限,过![]() 作抛物线
作抛物线![]() 的准线的垂线,
的准线的垂线,![]() 为垂足,且
为垂足,且![]() ,直线
,直线![]() 与直线
与直线![]() 关于直线
关于直线![]() 对称,求直线
对称,求直线![]() 的方程;
的方程;
(2)过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() 与
与![]() 面积之和为
面积之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的参数方程为: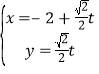 ,
,![]() 为参数
为参数![]() 点的极坐标为
点的极坐标为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
![]() Ⅱ
Ⅱ![]() 设直线l与曲线C相交于两点A,B,点M为AB的中点,求
设直线l与曲线C相交于两点A,B,点M为AB的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)设函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)如果对所有的![]() ≥0,都有
≥0,都有![]() ≤
≤![]() ,求
,求![]() 的最小值;
的最小值;
(Ⅲ)已知数列![]() 中,
中, ![]() ,且
,且![]() ,若数列
,若数列![]() 的前n项和为
的前n项和为![]() ,求证:
,求证:
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com