
【题目】(2015![]() 福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.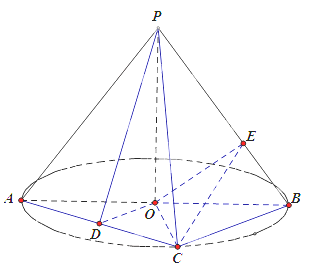
(1)若D为线段AC的中点,求证AC![]() 平面PDO;
平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若BC=![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
【答案】
(1)
详见解析;
(2)
![]() ;
;
(3)
![]() ;
;
【解析】解法一:(1)在![]() AOC中,因为OA=OC,D为AC的中点,所以AC
AOC中,因为OA=OC,D为AC的中点,所以AC![]() OD,又PO垂直于O所在平面,所以PO
OD,又PO垂直于O所在平面,所以PO![]() AC。 因为DO
AC。 因为DO![]() PO=0,所以AC
PO=0,所以AC![]() 平面PDO;
平面PDO;
(2)因为点C是圆O上,所以当CO![]() AB时,C到AB的距离最大,且最大值为1. 又AB=2,所以
AB时,C到AB的距离最大,且最大值为1. 又AB=2,所以![]() ABC的面积的最大值是
ABC的面积的最大值是![]()
![]() =1. 又因为三棱锥P-ABC的高PO=1,故三棱锥P-ABC体积的最大值为
=1. 又因为三棱锥P-ABC的高PO=1,故三棱锥P-ABC体积的最大值为![]() =
=![]()
(3)在![]() POB中,PO=OB=1,
POB中,PO=OB=1,![]() POB=
POB=![]() ,所以PB=
,所以PB=![]() =
=![]() ,同理PC=
,同理PC=![]() ,所以PB=PC=BC,在三棱锥P-ABC,将侧面BCP绕PB旋转至平面BC'P,使之与平面ABP共面,如图所示,当O,E,C'共线时,CE+OE取得最小值。又因为OP=OB,C'P=C'B,所以OC'垂直平分BP,即E为BP中点,从而OC'=OE+EC'=
,所以PB=PC=BC,在三棱锥P-ABC,将侧面BCP绕PB旋转至平面BC'P,使之与平面ABP共面,如图所示,当O,E,C'共线时,CE+OE取得最小值。又因为OP=OB,C'P=C'B,所以OC'垂直平分BP,即E为BP中点,从而OC'=OE+EC'=![]() +
+![]() =
=![]() ,亦即CE+OE的最小值为
,亦即CE+OE的最小值为![]() 。
。
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】
A.16
B.18
C.25
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)设![]() . 若p:
. 若p:![]() 成等比数列;
成等比数列;
q:![]() ,则( )
,则( )
A.p是q的充分条件,但不是q的必要条件
B.p是q的必要条件,但不是q的充分条件
C.p是q的充分必要条件
D.p既不是q的充分条件,也不是q的必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)已知数列![]() 的各项均为正数,
的各项均为正数,![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的单调区间,并比较
的单调区间,并比较![]() 与
与![]() 的大小;
的大小;
(2)计算![]() ,
, ![]() ,
, ![]() , 由此推测计算
, 由此推测计算![]() 的公式,并给出证明;
的公式,并给出证明;
(3)令![]() , 数列
, 数列![]() ,
, ![]() 的前
的前![]() 项和分别记为
项和分别记为![]() ,
,![]() , 证明:
, 证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)一种画椭圆的工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆ON可绕O转动,长杆MN通过N处铰链
的中点,短杆ON可绕O转动,长杆MN通过N处铰链
与ON连接,MN上的栓子D可沿滑槽AB滑动,且![]() ,
,![]() .当栓子D在滑槽AB内作往复运动时,带动N绕
.当栓子D在滑槽AB内作往复运动时,带动N绕![]() 转动,M处的笔尖画出的椭圆记为C.以O为原点,AB所在的直线为
转动,M处的笔尖画出的椭圆记为C.以O为原点,AB所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
(1)(Ⅰ)求椭圆C的方程;
(2)(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与椭圆
总与椭圆![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.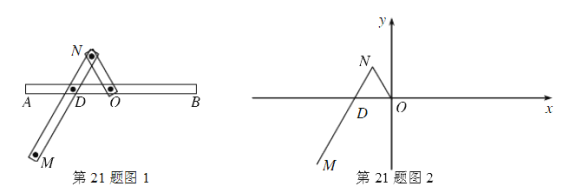
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)某工作的三视图如图3所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积/原工件的体积)
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com