
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,等差数列
,等差数列![]() 满足
满足![]() .
.
(1)分别求数列![]() 的通项公式;
的通项公式;
(2)若对任意的![]() ,恒成立,求实数
,恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)由![]() ----①得
----①得![]() ----②,
----②,
①![]() ②得
②得![]() ,
,![]()
又a2=3,a1=1也满足上式,∴an=3n-1;----------------3分
![]() ; -----------------6分
; -----------------6分
(2)![]() ,
,
![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,-----8分
恒成立,-----8分
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,--------------10分
,--------------10分
![]() ,
,![]() .----------12分
.----------12分
【解析】
试题(1)根据条件等差数列![]() 满足
满足![]() ,
,![]() ,将其转化为等差数列基本量
,将其转化为等差数列基本量![]() 的求解,从而可以得到
的求解,从而可以得到![]() 的通项公式,根据
的通项公式,根据![]() 可将条件中的
可将条件中的![]() 变形得到
变形得到![]() ,验证此递推公式当n=1时也成立,可得到
,验证此递推公式当n=1时也成立,可得到![]() 是等比数列,从而得到
是等比数列,从而得到![]() 的通项公式;
的通项公式;
(2)根据(1)中所求得的通项公式,题中的不等式![]() 可转化为
可转化为![]() ,从而问题等价于求
,从而问题等价于求![]() ,可求得当n=3时,为最大项,从而可以得到
,可求得当n=3时,为最大项,从而可以得到![]() .
.
(1)设等差数列![]() 公差为
公差为![]() ,则
,则![]() ,
,
解得![]() ,
,![]() , (2分)
, (2分)
当![]() 时,
时,![]() ,则
,则![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 是以1为首项3为公比的等比数列,则
是以1为首项3为公比的等比数列,则![]()
![]() . (6分);
. (6分);
(2)由(1)知,![]() ,原不等式可化为
,原不等式可化为![]() (8分)
(8分)
若对任意的![]() 恒成立,
恒成立,![]() ,问题转化为求数列
,问题转化为求数列![]() 的最大项
的最大项
令![]() ,则
,则![]() ,解得
,解得![]() ,所以
,所以![]() , (10分)
, (10分)
即![]() 的最大项为第
的最大项为第![]() 项,
项,![]() ,所以实数
,所以实数![]() 的取值范围
的取值范围![]() . (12分).
. (12分).


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】(2015·四川)某市A,B两所中学的学生组队参加辩论赛,A中学推荐3名男生,2名女生,B中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队。
(1)求A中学至少有1名学生入选代表队的概率.
(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X得分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
据茎叶图能得到的统计结论的标号为( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)一种作图工具如图1所示.O是滑槽AB的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且![]() ,
,![]() .当栓子D在滑槽AB内作往复运动时,带动N绕O转动一周(D不动时,N也不动),M处的笔尖画出的曲线记为C.以O为原点,AB所在的直线为
.当栓子D在滑槽AB内作往复运动时,带动N绕O转动一周(D不动时,N也不动),M处的笔尖画出的曲线记为C.以O为原点,AB所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
(1)求曲线C的方程;
(2)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与曲线C有且只有一个公共点,试探究:
总与曲线C有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015![]() 福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.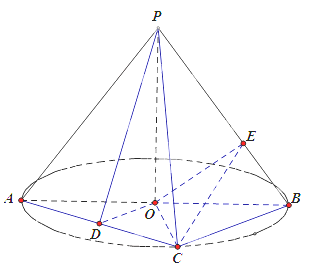
(1)若D为线段AC的中点,求证AC![]() 平面PDO;
平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若BC=![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,求解下列问题:(1)求
,求解下列问题:(1)求![]() 的单调区间;(2)在锐角 △ A B C 中,角 ∠ A , B , C ,的对边分别为 a , b , c ,若
的单调区间;(2)在锐角 △ A B C 中,角 ∠ A , B , C ,的对边分别为 a , b , c ,若 ![]() = 0 , a = 1 ,求 △ A B C 面积的最大值.
= 0 , a = 1 ,求 △ A B C 面积的最大值.
(1)求![]() 的单调区间;
的单调区间;
(2)在锐角![]() 中,角
中,角![]() ,的对边分别为
,的对边分别为![]() ,若
,若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点. 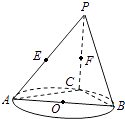
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足 ![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com