
【题目】下列函数中,既是偶函数又存在零点的是
A.y=COSx
B.y=SINx
C.y=lnx
D.y=![]() +1
+1
【答案】A
【解析】由选项可知,B,C项均不是偶函数,故排除B,C,A,D项是偶函数,但D与x轴没有交点,即D项的函数不存在零点,故选A.
【考点精析】认真审题,首先需要了解函数的概念及其构成要素(函数三要素是定义域,对应法则和值域,而定义域和对应法则是起决定作用的要素,因为这二者确定后,值域也就相应得到确定,因此只有定义域和对应法则二者完全相同的函数才是同一函数),还要掌握函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇)的相关知识才是答题的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:
【题目】(2015·湖南)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球A1, A2和1个白球B的甲箱与装有2个红球a1,a2和2个白球b1,b2的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
(1)用球的标号列出所有可能的摸出结果;
(2)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() , 点
, 点![]() 在椭圆上且位于第一象限,直线
在椭圆上且位于第一象限,直线![]() 被圆
被圆![]() 截得的线段的长为
截得的线段的长为![]() .(1)求直线 F M 的斜率(2)求椭圆的方程(3)设动点 P 在椭圆上,若直线FP的斜率大于
.(1)求直线 F M 的斜率(2)求椭圆的方程(3)设动点 P 在椭圆上,若直线FP的斜率大于![]() ,求直线OP( O 为原点)的斜率的取值范围
,求直线OP( O 为原点)的斜率的取值范围
(1)求直线![]() 的斜率
的斜率
(2)求椭圆的方程
(3)设动点![]() 在椭圆上,若直线
在椭圆上,若直线![]() 的斜率大于
的斜率大于![]() , 求直线
, 求直线![]() (
(![]() 为原点)的斜率的取值范围
为原点)的斜率的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)一种画椭圆的工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆ON可绕O转动,长杆MN通过N处铰链
的中点,短杆ON可绕O转动,长杆MN通过N处铰链
与ON连接,MN上的栓子D可沿滑槽AB滑动,且![]() ,
,![]() .当栓子D在滑槽AB内作往复运动时,带动N绕
.当栓子D在滑槽AB内作往复运动时,带动N绕![]() 转动,M处的笔尖画出的椭圆记为C.以O为原点,AB所在的直线为
转动,M处的笔尖画出的椭圆记为C.以O为原点,AB所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
(1)(Ⅰ)求椭圆C的方程;
(2)(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与椭圆
总与椭圆![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.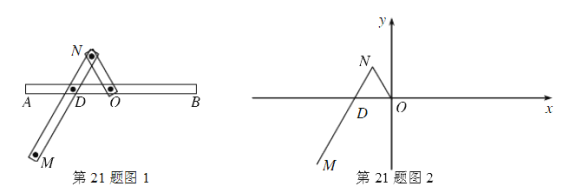
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线表示),则原始的最大流量与当前最大流量的比值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示,若将运动员按成绩由好到差编为![]() 号,再用系统抽样方法从中抽取7人,则其中成绩在区间
号,再用系统抽样方法从中抽取7人,则其中成绩在区间![]() 上的运动员人数是
上的运动员人数是 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+a|+|x﹣2|
(1)当a=﹣3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x﹣4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com