
【题目】![]() 设
设![]() ,Xn是曲线y=X2n+2+1在点(1,2)处的切线与x轴焦点的横坐标
,Xn是曲线y=X2n+2+1在点(1,2)处的切线与x轴焦点的横坐标
(1)求数列{xn}的通项公式;
(2)记Tn=![]()
![]() ....
....![]() ,证明Tn
,证明Tn![]()
【答案】
(1)
Xn=1-![]() =
=![]()
(2)
证明:由题设和(1)中的计算结果知
TN=![]()
![]() ....
....![]() =(
=(![]() )2(
)2(![]() )2...(
)2...(![]() )2
)2
当n=1,T1=![]() ,当n
,当n![]() 2时,因为
2时,因为![]() =
=![]() ,所以Tn
,所以Tn![]()
![]()
综上所述,n![]() ,均有Tn
,均有Tn![]() 要证Tn
要证Tn![]() ,需考虑通项X2n-12,通过适当放缩能够使得每项相消即可证明均有Tn
,需考虑通项X2n-12,通过适当放缩能够使得每项相消即可证明均有Tn![]()
证明:由题设和(1)中的计算结果知
TN=![]()
![]() ....
....![]() =(
=(![]() )2(
)2(![]() )2...(
)2...(![]() )2
)2
当n=1时,T1=![]() ,当n
,当n![]() 2时,因为
2时,因为![]() =
=![]() ,所以Tn
,所以Tn![]()
![]()
综上所述,![]() ,均有Tn
,均有Tn![]()
【解析】
1、求导得,y'=(2x+2)x2n+1,因为x=1,所以k=2n+2,从而在(1,2)处的切线方程为y-2= (2n+2)(x-1),
令y=0,解得切线与x轴交点的横坐标Xn=1-![]() =
=![]() 。
。
2、证明:由题设和(1)中的计算结果知
TN=![]()
![]() ....
....![]() =(
=(![]() )2(
)2(![]() )2...(
)2...(![]() )2
)2
当n=1,T1=![]() , 当n
, 当n![]() 2时,因为
2时,因为![]() =
=![]() ,所以Tn
,所以Tn![]()
![]()
综上所述,n![]() ,均有Tn
,均有Tn![]() 要证Tn
要证Tn![]() ,需考虑通项X2n-12,通过适当放缩能够使得每项相消即可证明均有Tn
,需考虑通项X2n-12,通过适当放缩能够使得每项相消即可证明均有Tn![]()
证明:由题设和(1)中的计算结果知
TN=![]()
![]() ....
....![]() =(
=(![]() )2(
)2(![]() )2...(
)2...(![]() )2
)2
当n=1时,T1=![]() ,当n
,当n![]() 2时,因为
2时,因为![]() =
=![]() ,所以Tn
,所以Tn![]()
![]()
综上所述,![]() ,均有Tn
,均有Tn![]()
【考点精析】利用等差数列的通项公式(及其变式)对题目进行判断即可得到答案,需要熟知通项公式:![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】若![]() ,m 是两条不同的直线,m 垂直于平面
,m 是两条不同的直线,m 垂直于平面![]() ,则“
,则“![]() ”是“
”是“![]() " 的 ( )
" 的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
在如图所示的阳马P-ABCD中,侧棱PD![]() 底面ABCD,且PD=CD,点E是BC的中点,连接DE,BD,BE
底面ABCD,且PD=CD,点E是BC的中点,连接DE,BD,BE
(I)证明:DE![]() 底面PBC,试判断四面体EBCD是否为鳖臑. 若是,写出其四个面的直角(只需写出结论);若不是,请说明理由;
底面PBC,试判断四面体EBCD是否为鳖臑. 若是,写出其四个面的直角(只需写出结论);若不是,请说明理由;
(Ⅱ)记阳马![]() 的体积为
的体积为![]() ,四面体
,四面体![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.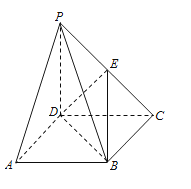
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)设f(x)=lnx, 0<a<b,若p=f(![]() ),q=f(
),q=f(![]() ),r=
),r=![]() (f(a)+f(b)),则下列关系式中正确的是( )
(f(a)+f(b)),则下列关系式中正确的是( )
A.q=r<p
B.q=r>p
C.p=r<q
D.p=r>q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)已知椭圆E: ![]() (a>b>0)的半焦距为c,原点0到经过两点(c,0),(0,b)的直线的距离为
(a>b>0)的半焦距为c,原点0到经过两点(c,0),(0,b)的直线的距离为![]() c.
c.
(1)求椭圆E的离心率
(2)如图,AB是圆M:(x+2)2+(y-1)=![]() 的一条直径,若椭圆E经过A,B两点,求椭圆E的方程.
的一条直径,若椭圆E经过A,B两点,求椭圆E的方程.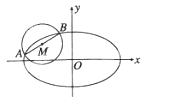
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:x2=4y 的焦点F也是椭圆c2:![]() 的一个焦点, C1和C2的公共弦长为
的一个焦点, C1和C2的公共弦长为![]()
(1)求 C2的方程;
(2)过点F 的直线 l与 C1相交于A与B两点, 与C2相交于C , D两点,且![]() 与
与![]() 同向
同向
(ⅰ)若 ![]() 求直线l的斜率;
求直线l的斜率;
(ⅱ)设 C1在点 A处的切线与 x轴的交点为M ,证明:直线l 绕点 F旋转时, ![]() MFD总是钝角三角形。
MFD总是钝角三角形。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中的内角A,B,C的对边分别为a,b,c,若 ![]() b=4c,B=2C (Ⅰ)求cosB;
b=4c,B=2C (Ⅰ)求cosB;
(Ⅱ)若c=5,点D为边BC上一点,且BD=6,求△ADC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com