Question

【题目】(2015·陕西）已知椭圆E: （a>b>0）的半焦距为c，原点0到经过两点(c,0)，(0,b)的直线的距离为c．
（1）求椭圆E的离心率
（2）如图，AB是圆M：（x+2）2+（y-1)=的一条直径，若椭圆E经过A,B两点，求椭圆E的方程．

Answer 1

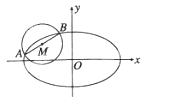
【答案】
（1）

（2）

【解析】先写过点(c,0)，(0,b)的直线方程，再计算原点o到该直线的距离，进而可得椭圆E的离心率；（II）先由（I）知椭圆E的方程，设AB的方程，联立，消去y，可得x1+x2和x1x2的值，进而可得k，再利用|AB|=可得b2的值，进而可得椭圆E的方程．
试题解析：（I）过点(c,0),(0,b)的直线方程为bx+cy-bc=0，
则原点O到直线的距离d=，
由d=，得a=2b=2，解得离心率=.
(II)解法一：由（I）知，椭圆E的方程为.x2+4y2=4b2(1)
依题意，圆心M(-2,1)是线段AB的中点，且|AB|=.
易知，AB不与x轴垂直，设其直线方程为y=k(x+2)+1，代入(1)得
(1+4k2)x2+8k(2k+1)x+4(2k+1)2-4b2=0
设A(x1,y1), B (x2, y2 ) 则x1+x2=-, x1·x2=-
由x1+x2=-4，得==-4解得k=
从而.x1·x2=8-2b2.
于是.|AB|=|x1-x2|==
由|AB|=，得=，解得b2=3
故椭圆E的方程为
解法二：由（I）知，椭圆E的方程为x2+4y2=4b2. (2)
依题意，点A，B关于圆心M(-2,1)对称，且|AB|=.
设A(x1,y1), B (x2, y2 )则，x12+4y12=4b2 ， x22+y22=4b2
两式相减并结合x1+x2=-4, y1+y2=2得-4(x1-x2)+8(y1-y2)=0.
易知，AB不与x轴垂直，则x1≠x2 ， 所以AB的斜率kAB==
因此AB直线方程为y=(x+2)+1，代入(2)得x2+4x+8-2b2=0
所以，x1+x2=-4, x1·x2=8-2b2.
于是.|AB|=|x1-x2|==
由|AB|=，得=，解得b2=3.
故椭圆E的方程为.