
 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD中点,连结AG分别交⊙O、BD于点E、F连结CE.
如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD中点,连结AG分别交⊙O、BD于点E、F连结CE.
(1)求证: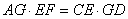 ;
;
(2)求证: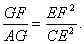
1) 若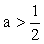 ,令
,令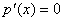 ,得极值点
,得极值点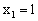 ,
,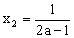 ,
,
当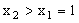 ,即
,即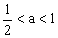 时,在(
时,在(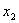 ,+∞)上有
,+∞)上有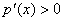 ,此时
,此时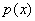 在区间(
在区间(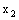 ,+∞)上是增函数,并且在该区间上有
,+∞)上是增函数,并且在该区间上有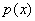 ∈(
∈(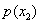 ,+∞),不合题意;
,+∞),不合题意;
当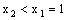 ,即
,即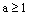 时,同理可知,
时,同理可知,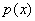 在区间(1,+∞)上,有
在区间(1,+∞)上,有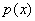 ∈(
∈(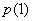 ,+∞),也不合题意;
,+∞),也不合题意;
2) 若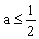 ,则有
,则有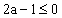 ,此时在区间(1,+∞)上恒有
,此时在区间(1,+∞)上恒有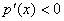 ,从而
,从而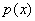 在区间(1,+∞)
在区间(1,+∞)
上是减函数;要使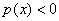 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足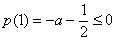
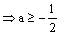 ,
,
所以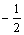
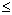 a
a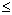
 .
.
又因为h/(x)= –x+2a– =
= 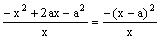 <0, h(x)在(1, +∞)上为减函数,
<0, h(x)在(1, +∞)上为减函数,
h(x)<h(1)= 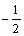 +2a
+2a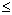 0, 所以a
0, 所以a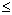
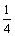 综合可知
综合可知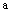 的范围是[
的范围是[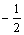 ,
,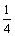 ]. 12分
]. 12分
另解:(接在(*)号后)先考虑h(x), h`(x) = – x + 2a 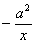 =
=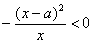 ,
,
h(x)在(1,+)递减,只要h(1) 0, 得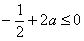 ,解得
,解得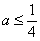 . 而p`(x)=
. 而p`(x)=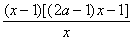 对x(1,+) 且
对x(1,+) 且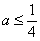 有p`(x) <0.
有p`(x) <0.
只要p(1) 0, 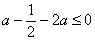 ,解得
,解得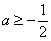 ,所以.
,所以.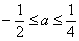 。
。


科目:高中数学 来源: 题型:
从3名语文老师、4名数学老师和5名英语老师中选派5人组成一个支教小组,则语文、数学和英语老师都至少有1人的选派方法种数是( )
A.590 B.570 C.360 D.210
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com