
| A. | $\frac{5}{21}$ | B. | $\frac{5}{42}$ | C. | $\frac{8}{21}$ | D. | $\frac{4}{21}$ |
分析 本题是一道平均分组问题,将7个人(含甲、乙)分成三个组,一组3人,另两组2人,有两个组都是两个人,而这两个组又没有区别,所以分组数容易重复,甲、乙分到同一组的概率要分类计算
解答 解:不同的分组数为a=$\frac{{C}_{7}^{3}{{C}_{4}^{2}C}_{2}^{2}}{2!}$=105
甲、乙分在同一组的方法种数有
(1)若甲、乙分在3人组,有$\frac{{C}_{5}^{1}{{C}_{4}^{2}C}_{2}^{2}}{2!}$=15种
(2)若甲、乙分在2人组,有C53=10种,故共有25种,
所以P=$\frac{25}{105}=\frac{5}{21}$.
故选:A
点评 平均分组问题是概率中最困难的问题,解题时往往会忽略有些情况是相同的


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{3}}}{4}$ | B. | $\frac{{3\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{3\sqrt{6}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24$\sqrt{2}$ | B. | 8 | C. | 8$\sqrt{2}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,$CD=\sqrt{3}$,平面PAD⊥底面ABCD,若M为AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,$CD=\sqrt{3}$,平面PAD⊥底面ABCD,若M为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=2为f(x)的极小值点 | B. | x=2为f(x)的极大值点 | ||
| C. | $x=\frac{1}{2}$为f(x)的极小值点 | D. | $x=\frac{1}{2}$为f(x)的极大值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(理)试卷(解析版) 题型:选择题
定义域为 的连续可导函数
的连续可导函数 ,若满足以下两个条件:
,若满足以下两个条件:
① 的导函数
的导函数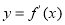 没有零点,
没有零点,
②对 ,都有
,都有 .
.
则关于 方程
方程 有( )个解.
有( )个解.
A.2 B.1 C.0 D.以上答案均不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com