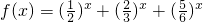练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    研究函数数学公式的单调性，并求解方程：3x+4x+5x=6x．

    解：∵0＜＜1，0＜＜1，0＜＜1，
    ∴y=、y=、y=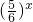 都是减函数，故 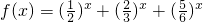在其定义域
    内是减函数．
    ∵x=3时，3x+4x+5x=216，63=216，令 y（x）=3x+4x+5x-6x，
    由y（x）的导数大于0知，y（x）是一个增函数，y（2）=50-36＞0，y（4）=962-1296＜0，
    故 3x+4x+5x=6x 的解是 x=3．
    分析：由y=、y=、y=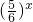 都是减函数可得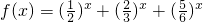是减函数，令 y（x）=3x+4x+5x-6x，由y（x）的导数大于0知，y（x）是一个增函数，y（2）＞0，y（4）＜0，y（3）=0，可得答案．
    点评：本题考查指数函数单调性和特殊点，几个单调减函数的和还是减函数，指数方程的解法．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本题16分）已知函数有如下性质：如果常数，那么该函数在上是减函数，在上是增函数。

    （1）如果函数在上是减函数，在上是增函数，求的值。

    （2）设常数，求函数的最大值和最小值；

    （3）当是正整数时，研究函数的单调性，并说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题16分）已知函数有如下性质：如果常数，那么该函数在上是减函数，在上是增函数。

    （1）如果函数在上是减函数，在上是增函数，求的值。

    （2）设常数，求函数的最大值和最小值；

    （3）当是正整数时，研究函数的单调性，并说明理由  

    查看答案和解析>>

    科目：高中数学 来源：2013届浙江省温州市高二第二学期期中考试理科数学（解析版） 题型：解答题

    已知函数，，k为非零实数.

    （Ⅰ）设t=k2,若函数f(x),g(x)在区间(0,+∞)上单调性相同，求k的取值范围;

    （Ⅱ）是否存在正实数k，都能找到t∈[1,2],使得关于x的方程f(x)=g(x)在[1,5]上有且仅有一个实数根，且在[－5,－1]上至多有一个实数根.若存在，请求出所有k的值的集合；若不存在，请说明理由.

     

    【解析】本试题考查了运用导数来研究函数的单调性，并求解参数的取值范围。与此同时还能对于方程解的问题，转化为图像与图像的交点问题来长处理的数学思想的运用。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

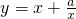    已知函数数学公式有如下性质：如果常数a＞0，那么该函数在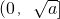数学公式上是减函数，在数学公式上是增函数．
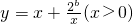    （1）如果函数数学公式在（0，4]上是减函数，在[4，+∞）上是增函数，求b的值．
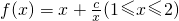    （2）设常数c∈[1，4]，求函数数学公式的最大值和最小值；
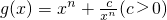    （3）当n是正整数时，研究函数数学公式的单调性，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2006年上海市高考数学试卷（文科）（解析版） 题型：解答题

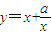    已知函数有如下性质：如果常数a＞0，那么该函数在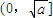上是减函数，在上是增函数．
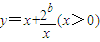    （1）如果函数在（0，4]上是减函数，在[4，+∞）上是增函数，求b的值．
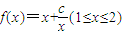    （2）设常数c∈[1，4]，求函数的最大值和最小值；
    （3）当n是正整数时，研究函数的单调性，并说明理由．

    查看答案和解析>>

    同步练习册答案