
根据如下样本数据
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 |
| 0.5 |
|
得到的回归方程为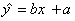 .若
.若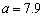 ,则
,则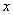 每增加1个单位,
每增加1个单位,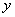 就 ( )
就 ( )
A.增加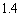 个单位; B.减少
个单位; B.减少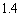 个单位; C.增加
个单位; C.增加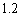 个单位; D.减少
个单位; D.减少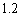 个单位.
个单位.
科目:高中数学 来源: 题型:
某供货商拟从码头 发货至其对岸
发货至其对岸 的两个商场
的两个商场 ,
, 处,通常货物先由
处,通常货物先由 处船运至
处船运至 之间的中转站
之间的中转站 ,再利用车辆转运.如图,码头
,再利用车辆转运.如图,码头 与两商场
与两商场 ,
, 的距离相等,两商场间的距离为
的距离相等,两商场间的距离为 千米,且
千米,且 .若一批货物从码头
.若一批货物从码头 至
至 处的运费为100元/千米,这批货到
处的运费为100元/千米,这批货到 后需分别发车2辆、4辆转运至
后需分别发车2辆、4辆转运至 、
、 处,每辆汽车运费为25元/千米.设
处,每辆汽车运费为25元/千米.设 该批货总运费为
该批货总运费为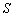 元.
元.
(Ⅰ)写出 关于
关于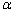 的函数关系式,并指出
的函数关系式,并指出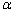 的取值范围;
的取值范围;
(Ⅱ)当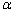 为何值时,总运费
为何值时,总运费 最小?并求出
最小?并求出 的最小值.
的最小值.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
学习合情推理后,甲、乙两位同学各举一个例子. 甲:由“若三角形周长为 ,面积为
,面积为 ,则其内切圆半径r =
,则其内切圆半径r = ”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径r =
”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径r = ”;乙:由“若直角三角形两直角边长分别为
”;乙:由“若直角三角形两直角边长分别为 ,则其外接圆半径r =
,则其外接圆半径r = ” 类比可得“若三棱锥三条侧棱两两垂直, 侧棱长分别为
” 类比可得“若三棱锥三条侧棱两两垂直, 侧棱长分别为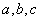 ,则其外接球半径r =
,则其外接球半径r = ”。这两位同学类比得出的结论判断正确的是 .(请将序号填写在横线上)
”。这两位同学类比得出的结论判断正确的是 .(请将序号填写在横线上)
①甲对 ②乙对 ③ 甲错 ④乙错
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题错误的是( ).
A.命题“若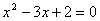 ,则
,则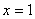 ”的逆否命题为“若
”的逆否命题为“若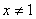 ,则
,则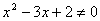 ”
”
B.若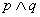 为假命题,则
为假命题,则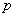 、
、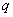 均为假命题
均为假命题
C.命题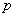 :存在
:存在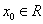 ,使得
,使得 ,则
,则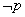 :任意
:任意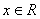 ,都有
,都有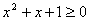
D.“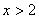 ”是“
”是“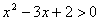 ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com