
设数列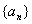 的前n项和为
的前n项和为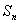 ,且
,且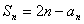 (
(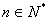 ).
).
(1)求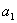 ,
,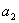 ,
,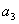 ,
,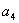 的值;
的值;
(2)猜想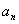 的表达式,并加以证明.
的表达式,并加以证明.
科目:高中数学 来源: 题型:
用边长为48厘米的正方形铁皮做一个无盖的铁盒时,在铁皮的四角各截去一个面积相等的小正方形,然后把四边折起,就能焊成铁盒. 当所做的铁盒的容积最大时,在四角截去的正方形的边长为 ( )
A.12 B. 10 C. 8 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
根据如下样本数据
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 |
| 0.5 |
|
得到的回归方程为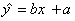 .若
.若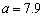 ,则
,则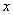 每增加1个单位,
每增加1个单位,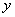 就 ( )
就 ( )
A.增加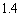 个单位; B.减少
个单位; B.减少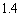 个单位; C.增加
个单位; C.增加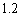 个单位; D.减少
个单位; D.减少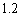 个单位.
个单位.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com