
分析 先根据复数相等确定a,b的值,再直接运用定积分计算公式求解.
解答 解:因为$\frac{2i}{1-i}+ai=b-2i(a,b∈R)$,
所以-1+(a+1)i=b-2i,
即b=-1且a+1=-2,解得$\left\{\begin{array}{l}{a=-3}\\{b=-1}\end{array}\right.$,所以,
$\int_{\;\;a}^{\;b}{(3{x^2}}-2)dx$=${∫}_{-3}^{-1}$(3x2-2)dx
=$(x^3-2x){|}_{-3}^{-1}$
=(1)-(-21)=22,
所以,原式的值为22,
故答案为:22.
点评 本题主要考查了复数的代数运算以及定积分的求解,涉及复数的四则运算和多项式函数定积分的运算,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
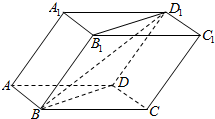 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则直线BD1与平面ABCD所成的角的正切值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{\sqrt{39}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | $\frac{{\sqrt{21}}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $13\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+x | B. | -x2+x | C. | -x2-x | D. | x2-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com