
分析 (1)由已知得到对应方程的根为1,2,代入对应方程求得a;
(2)当a>0时,不等式f(x)<0等价于(x-$\frac{1}{a}$)(x-1)<0,针对$\frac{1}{a}$与1的关系讨论根的大小,得到不等式的解集.
解答 解:(1)依题意知a>0且1和2为方程(ax-1)(x-1)=0的两根,∴$\frac{1}{a}=2$,∴$a=\frac{1}{2}$
(2)不等式f(x)<0可化为(ax-1)(x-1)<0.,
当a>0时,不等式f(x)<0等价于(x-$\frac{1}{a}$)(x-1)<0,
①当0<a<1时,$\frac{1}{a}$>1,
不等式(x-$\frac{1}{a}$)(x-1)<0,的解集为{x|1<x<$\frac{1}{a}$},
即原不等式的解集为{x|1<x<$\frac{1}{a}$},
②当a=1时,不等式(x-$\frac{1}{a}$)(x-1)<0,的解集为∅,
即原不等式的解集为∅,
③当a>1时,不等式(x-$\frac{1}{a}$)(x-1)<0的解集为{x|$\frac{1}{a}$<x<1},
即原不等式的解集为{x|$\frac{1}{a}$<x<1}.
点评 本题考查了一元二次不等式与对应方程的关系以及讨论求一元二次不等式的解集;注意讨论的要不重不漏.


科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x2-4|x|+3,x∈R.
已知函数f(x)=x2-4|x|+3,x∈R.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
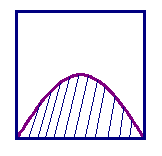 如图所示,墙上挂有一块边长为π的正方形木板,上面画有正弦曲线半个周期的图案(阴影部分).某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是( )
如图所示,墙上挂有一块边长为π的正方形木板,上面画有正弦曲线半个周期的图案(阴影部分).某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{π^2}$ | D. | $\frac{1}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=x,g(x)=\frac{{{x^2}-x}}{x-1}$ | B. | $f(x)=x,g(x)=\sqrt{x^2}$ | ||
| C. | f(x)=x2,g(x)=(x+1)2 | D. | $f(x)=x,g(x)=\root{3}{x^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com