练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知点列B1（1，b1），B2（2，b2），…，Bn（n，bn），…（n∈N）顺次为抛物线y=x2
    上的点，过点Bn（n，bn）作抛物线y=x2的切线交x轴于点An（an，0），点Cn（cn，0）在x轴上，且点An，Bn，Cn构成以点Bn为顶点的等腰三角形．
    （1）求数列{an}，{cn}的通项公式；
    （2）是否存在n使等腰三角形AnBnCn为直角三角形，
    若有，请求出n；若没有，请说明理由．
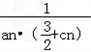    （3）设数列{}的前n项和为Sn，求证：≤Sn＜．
    解：∵y= x2，∴y′=，y′|x=n=，
    ∴点Bn（n，bn）作抛物线y=x2的切线方程为：y﹣=（x﹣n），
    令y=0，则x=，即an=；
    ∵点An，Bn，Cn构成以点Bn为顶点的等腰三角形，
    ∴an+cn=2n，∴cn=2n﹣an=  
    （2）解：若等腰三角形AnBnCn为直角三角形，
    则|AnCn|=2bn∴n=，∴n=2，
    ∴存在n=2，使等腰三角形A2B2C2为直角三角形  
    （3）证明：∵===（﹣）
    Sn=（1﹣+﹣+…+﹣）=（1﹣）＜
    又1﹣随n的增大而增大，
    ∴当n=1时，Sn的最小值为：（1﹣）=，
    ∴≤Sn＜
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知一列非零向量
    an
    ，n∈N*，满足：
    a1
    =（10，-5），
    an
    =(xn，yn)=k(xn-1-yn-1，xn-1+yn-1)    ，（n32 ）．，其中k是非零常数．
    （1）求数列{|
    an
    |}是的通项公式；
    （2）求向量
    an-1
    与
    an
    的夹角；（n≥2）；
    （3）当k=
    1
    2
    时，把
    a1
    ，
    a2
    ，…，
    an
    ，…中所有与
    a1
    共线的向量按原来的顺序排成一列，记为
    b1
    ，
    b2
    ，…，
    bn
    ，…，令
    OBn
    =
    b1
    +
    b2
    +…+
    bn
    ，O为坐标原点，求点列{Bn}的极限点B的坐标．（注：若点坐标为（tn，sn），且
    lim
    n→∞
    tn=t    ，
    lim
    n→∞
    sn=s    ，则称点B（t，s）为点列的极限点．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知一列非零向量
    an
    满足：
    a1
    =(x1，y1)，
    an
    =(xn，yn)=
    1
    2
    (xn-1-yn-1，xn-1+yn-1)(n≥2)    ．
    （Ⅰ）证明：{|
    an
    |}    是等比数列；
    （Ⅱ）求向量
    a
    n-1    与
    a
    n    的夹角(n≥2)    ；
    （Ⅲ）设
    a
    1    =(1，2)，把
    a1
    ，
    a2
    ，…，
    an
    ，…中所有与
    a1
    共线的向量按原来的顺序排成    一列，记为
    b1
    ，
    b2
    ，…，
    .
    bn
    ，…，令
    OB
    n    =
    b1
    +
    b2
    +…+
    bn
    ，0    为坐标原点，求点列{Bn}的极限点B的坐标．
    （注：若点Bn坐标为(tn，sn)，且
    lim
    n→∞
    tn=t，
    lim
    n→∞
    sn=s，则称点B(t，s)为点列{Bn}    的极限点．）

    查看答案和解析>>

    科目：高中数学 来源：2011届高考数学第一轮复习测试题9 题型：013

    数列{an}中a1＝1，a5＝13，an+2＋an＝2an+1；数列{bn}中，b2＝6，b3＝3，bn+2bn＝b，在直角坐标平面内，已知点列P1(a1，b1)，P2(a2，b2)，P3(a3，b3)，…，Pn(an，bn)…，则向量＋…＋P2009P2010的坐标为

    [　　]
    A．

    (3015，8[()1005－1])

    B．

    (3012)，8[()1005－1]

    C．

    (3015，8[()2010－1])

    D．

    (3018，8[()2010－1])

    查看答案和解析>>

    科目：高中数学 来源：0108 模拟题 题型：单选题

    数列{an}中a1=1，a5=13，an+2+an=2an+1；数列{bn}中，b2=6，b3=3，bn+2bn=b2n+1，在直角坐标平面内，已知点列P1（a1，b1），P2（a2，b2），P3（a3，b3），…，Pn（an，bn）…，则向量的坐标为
    [     ]
    A.（3015，8[（）1005-1]）
    B.（3012，[（）1005-1]）
    C.（3015，[（）2010-1]）
    D.（3018，[（）2010-1]）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{an}中a1=1，a5=13，an＋2＋an=2an+1；数列{bn}中，b2=6，b3=3，bn＋2bn=b2n+1,在直角坐标平面内，已知点列P1(a1，b1)，P2(a2，b2)，P3(a3，b3)，…，Pn(an，bn)，…，则向量＋＋＋…＋的坐标为（      ）

    A．                      B．

    C．                      D．

    查看答案和解析>>

    同步练习册答案