练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，互相垂直的两条公路AM、AN旁有一矩形花园ABCD，现欲将其扩建成一个更大的三角形花园APQ，要求P在射线AM上，Q在射线AN上，且PQ过点C，其中AB＝30m，AD＝20m.记三角形花园APQ的面积为S.

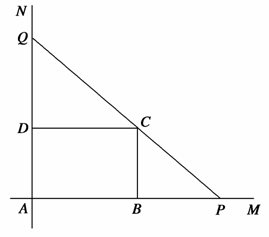
    (1)当DQ的长度是多少时，S最小？并求S的最小值；

    (2)要使S不小于1600m2，则DQ的长应在什么范围内？


    ＝15(x＋＋40)≥1200，当且仅当x＝20时取等号．

    (2)∵S≥1600，∴3x2－200x＋1200≥0，

    ∴0<x≤或x≥60.

    答：(1)当DQ的长度是20m时，S最小，且S的最小值为1200m2；

    (2)要使S不小于1600m2，则DQ的取值范围是0<DQ≤或DQ≥60.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知{an}为等差数列，{bn}为正项等比数列，公式q≠1，若a1＝b1，a11＝b11，则(　　)

    A．a6＝b6                                                     B．a6>b6

    C．a6<b6                                                       D．以上都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若关于x的不等式m(x－1)>x2－x的解集为{x|1<x<2}，则实数m的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在R上定义运算：＝ad－bc.若不等式≥1对任意实数x恒成立，则实数a的最大值为(　　)

    A．－                                                       B．－

    C.                                                              D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝4x＋(x>0，a>0)在x＝3时取得最小值，则a＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知b>0，直线(b2＋1)x＋ay＋2＝0与直线x－b2y－1＝0互相垂直，则ab的最小值等于(　　)

    A．1  B．2  C．2  D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若直线ax－by＋2＝0(a>0，b>0)被圆x2＋y2＋2x－4y＋1＝0截得的弦长为4，则＋的最小值为(　　)

    A.                                                             B.

    C.＋                                                    D.＋2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某公司准备进行两种组合投资，稳健型组合投资每份由金融投资20万元，房地产投资30万元组成；进取型组合投资每份由金融投资40万元，房地产投资30万元组成．已知每份稳健型组合投资每年可获利10万元，每份进取型组合投资每年可获利15万元．若可作投资用的资金中，金融投资不超过160万元，房地产投资不超过180万元，那么这两种组合投资各应注入多少份，才能使一年获利总额最多？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直线xsinα＋y＋2＝0的倾斜角的取值范围是(　　)

    查看答案和解析>>

    同步练习册答案