
分析 由正弦定理结合三角形内角的范围可求得sin2A=sin2B,根据和差化积公式整理求得cos(A+B)=0或sin(A-B)=0,推断出A+B=$\frac{π}{2}$或A=B,则三角形形状可判断出.
解答 解:∵由正弦定理可得:a=2RsinA,b=2RsinB,
∴$\frac{{a}^{2}}{{b}^{2}}$=$\frac{4{R}^{2}si{n}^{2}A}{4{R}^{2}si{n}^{2}B}$=$\frac{si{n}^{2}A}{si{n}^{2}B}$=$\frac{sinAcosB}{cosAsinB}$,
∵0<A<π,0<B<π,即sinA>0,sinB>0,
∴可得:$\frac{sinA}{sinB}=\frac{cosB}{cosA}$,解得sin2A=sin2B,
∴sin2A-sin2B=cos(A+B)sin(A-B)=0,
∴cos(A+B)=0或sin(A-B)=0,
∴A+B=$\frac{π}{2}$或A=B,
∴三角形为直角三角形或等腰三角形.
点评 本题主要考查了三角形的形状判断.需要挖掘题设信息,借助三角函数的基本公式和基本性质找到边与边或角与角之间的关系,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为e,过椭圆焦点F的直线l交椭圆于A、B两点,倾斜角为θ.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),离心率为e,过椭圆焦点F的直线l交椭圆于A、B两点,倾斜角为θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 志愿 | 第一志愿 | 第二志愿 | 第三志愿 |
| 学校 | 1 | 2 | 3 |
| 专业 | 第1专业 | 第1专业 | 第1专业 |
| 第2专业 | 第2专业 | 第2专业 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{(e-1)π}{2}$ | B. | $\frac{(e-1){π}}{3}$ | C. | $\frac{(e-1)π}{4}$ | D. | $\frac{(e-1)π}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
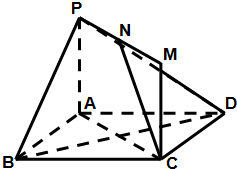 如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,
如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com