Question

18．已知函数f（x）=-x+2，
（1）判断函数的单调性并用定义证明；
（2）画出函数的图象．（直接描点画图）

Answer 1

分析 （1）先设在所给区间上有任意两个自变量x₁，x₂，且x₁＜x₂，再用作差法比较f（x₁）与f（x₂）的大小，做差后，应把差分解为几个因式的乘积的形式，通过判断每一个因式的正负，来判断积的正负，最后的出结论．
（2）由解析式，可得函数的图象．

解答 解：（1）此函数在R为减函数．…（2分）
证明：由原函数得定义域为R，
任取x₁，x₂∈R，且x₁＜x₂
∵f（x₁）-f（x₂）=（-x₁+2）-（-x₂+2）=x₂-x₁…（4分）
又∵x₁，x₂∈R，且x₁＜x₂，∴x₂-x₁＞0，即f（x₁）＞f（x₂）…（6分）
故函数f（x）=-x+2在R为减函数．…（8分）
（2）如图所示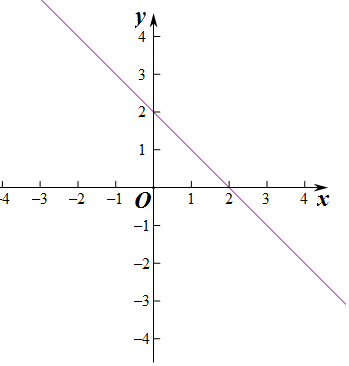
…（12分）

点评 本题主要考查了定义法证明函数的单调性，做题时应该严格按照步骤去做．