
 已知奇函数$f(x)=\left\{{\begin{array}{l}{-{x^2}+4x(x>0)}\\{0(x=0)}\\{{x^2}+mx(x<0)}\end{array}}\right.$
已知奇函数$f(x)=\left\{{\begin{array}{l}{-{x^2}+4x(x>0)}\\{0(x=0)}\\{{x^2}+mx(x<0)}\end{array}}\right.$分析 (1)根据函数是奇函数,结合函数的解析式即可求出m的值,
(2)根据图象得到函数的单调递增区间,利用函数f(x)在区间[-2,a-2]上单调递增,建立不等式,即可求得a的取值范围.
解答 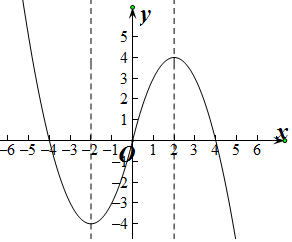 解:(1)∵f(x)为奇函数,
解:(1)∵f(x)为奇函数,
∴f(-x)=-f(x),
设x<0,则f(x)=x2+mx,
则-x>0,则f(-x)=-x2-4x=-f(x),
∴f(x)=x2+4x,
∴m=4,
图象如图所示:
(2)由图象可得,函数f(x)在[-2,2]上单调递增,
∵函数f(x)在区间[-2,a-2]上单调递增,
∴-2<a-2≤2,
解得0<a≤4,
故a的取值范围为(0,4]
点评 本题考查函数单调性与奇偶性的结合,考查学生的计算能力,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
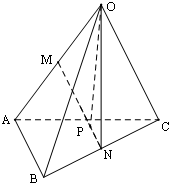 如图,M、N分别是四面体OABC的边OA,BC的中点,$\overrightarrow{MP}=3\overrightarrow{PN}$,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x、y、z的值分别为( )
如图,M、N分别是四面体OABC的边OA,BC的中点,$\overrightarrow{MP}=3\overrightarrow{PN}$,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x、y、z的值分别为( )| A. | $\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{3}$ | B. | $\frac{1}{3}$,$\frac{1}{6}$,$\frac{1}{6}$ | C. | $\frac{1}{8}$,$\frac{3}{8}$,$\frac{3}{8}$ | D. | $\frac{3}{8}$,$\frac{1}{8}$,$\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
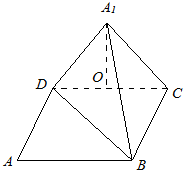 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1O⊥平面BCD.
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到A1点,且A1O⊥平面BCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com