
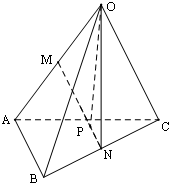
 如图,M、N分别是四面体OABC的边OA,BC的中点,$\overrightarrow{MP}=3\overrightarrow{PN}$,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x、y、z的值分别为( )
如图,M、N分别是四面体OABC的边OA,BC的中点,$\overrightarrow{MP}=3\overrightarrow{PN}$,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x、y、z的值分别为( )| A. | $\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{3}$ | B. | $\frac{1}{3}$,$\frac{1}{6}$,$\frac{1}{6}$ | C. | $\frac{1}{8}$,$\frac{3}{8}$,$\frac{3}{8}$ | D. | $\frac{3}{8}$,$\frac{1}{8}$,$\frac{1}{8}$ |
分析 根据向量的减法和共线向量基本定理及向量加法的平行四边形法则,用向量$\overrightarrow{OA}$、$\overrightarrow{OB}$和$\overrightarrow{OC}$表示出向量$\overrightarrow{OP}$,即可得到x、y、z的值.
解答 解:∵M、N分别是四面体OABC的边OA,BC的中点,
∴$\overrightarrow{OM}$=$\frac{1}{2}$$\overrightarrow{OA}$,$\overrightarrow{ON}$=$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$);
由$\overrightarrow{MP}=3\overrightarrow{PN}$,得$\overrightarrow{OP}$-$\overrightarrow{OM}$=3($\overrightarrow{ON}$-$\overrightarrow{OP}$),
∴$\overrightarrow{OP}$=$\frac{1}{4}$$\overrightarrow{OM}$+$\frac{3}{4}$$\overrightarrow{ON}$=$\frac{1}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OC}$,
又$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,
∴x=$\frac{1}{8}$、y=$\frac{3}{8}$、z=$\frac{3}{8}$.
故选:C.
点评 本题考查了向量的减法与平面向量基本定理,向量加法的平行四边形法则的应用问题,是基础题目.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=sin({2x+\frac{π}{3}})$ | B. | $f(x)=sin({2x+\frac{π}{6}})$ | C. | $f(x)=sin({\frac{1}{2}x+\frac{π}{3}})$ | D. | $f(x)=sin({\frac{1}{2}x+\frac{π}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知奇函数$f(x)=\left\{{\begin{array}{l}{-{x^2}+4x(x>0)}\\{0(x=0)}\\{{x^2}+mx(x<0)}\end{array}}\right.$
已知奇函数$f(x)=\left\{{\begin{array}{l}{-{x^2}+4x(x>0)}\\{0(x=0)}\\{{x^2}+mx(x<0)}\end{array}}\right.$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com