
| A. | $f(x)=sin({2x+\frac{π}{3}})$ | B. | $f(x)=sin({2x+\frac{π}{6}})$ | C. | $f(x)=sin({\frac{1}{2}x+\frac{π}{3}})$ | D. | $f(x)=sin({\frac{1}{2}x+\frac{π}{6}})$ |
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p:0=∅;q:0∈∅ | |
| B. | p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数 | |
| C. | p:a+b≥2$\sqrt{ab}$(a,b∈R);q:不等式|x|>x的解集为(-∞,0) | |
| D. | p:圆(x-1)2+(y-2)2=1的面积被直线x=1平分;q:椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的离心率为e=$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinα)>f(cosβ) | B. | f(sinα)>f(sinβ) | C. | f(cosα)>f(cosβ) | D. | f(cosα)>f(sinβ) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
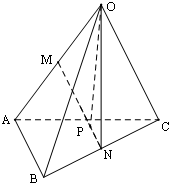 如图,M、N分别是四面体OABC的边OA,BC的中点,$\overrightarrow{MP}=3\overrightarrow{PN}$,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x、y、z的值分别为( )
如图,M、N分别是四面体OABC的边OA,BC的中点,$\overrightarrow{MP}=3\overrightarrow{PN}$,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$,则x、y、z的值分别为( )| A. | $\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{3}$ | B. | $\frac{1}{3}$,$\frac{1}{6}$,$\frac{1}{6}$ | C. | $\frac{1}{8}$,$\frac{3}{8}$,$\frac{3}{8}$ | D. | $\frac{3}{8}$,$\frac{1}{8}$,$\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ln2 | C. | 1 | D. | $\root{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com