
| A. | 2 | B. | ln2 | C. | 1 | D. | $\root{3}{2}$ |
分析 对f(x)求导,并令导函数为零,可得极值点$x=\frac{{ln\frac{a}{b}}}{b}$,代入函数f(x),则$f(\frac{{ln\frac{a}{b}}}{b})=\frac{a}{b}(1-ln\frac{a}{b})$=1(极小值,因为f(x)的二阶导数恒大于0),得到$1-ln\frac{a}{b}=\frac{b}{a}$,考察方程$1-lnx=\frac{1}{x}$,即$lnx=1-\frac{1}{x}$,画出函数y=lnx和函数$y=1-\frac{1}{x}$,可求得x=1,即可得出结论.
解答 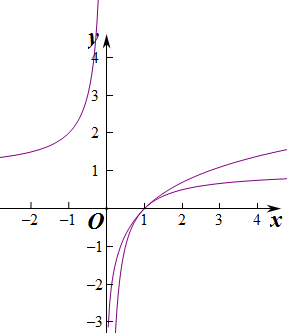 解:对f(x)求导,f′(x)=bebx-a,
解:对f(x)求导,f′(x)=bebx-a,
令导函数为零,即f′(x)=bebx-a=0,可得极值点$x=\frac{{ln\frac{a}{b}}}{b}$,
代入函数f(x),则$f(\frac{{ln\frac{a}{b}}}{b})=\frac{a}{b}(1-ln\frac{a}{b})$=1,得到$1-ln\frac{a}{b}=\frac{b}{a}$,
考察方程$1-lnx=\frac{1}{x}$,即$lnx=1-\frac{1}{x}$,
画出函数y=lnx和函数$y=1-\frac{1}{x}$,可求得x=1,
因而$\frac{b}{a}=1$.
故选:C.
点评 本题考查导数知识的综合运用,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=sin({2x+\frac{π}{3}})$ | B. | $f(x)=sin({2x+\frac{π}{6}})$ | C. | $f(x)=sin({\frac{1}{2}x+\frac{π}{3}})$ | D. | $f(x)=sin({\frac{1}{2}x+\frac{π}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com