
���� �ֱ����ֱ�ߵ�ƽ�кʹ�ֱ�жϼ��ɣ�
��� �⣺ֱ��A1x+B1y+C1=0�ķ�������Ϊ��-B1��A1����
ֱ��A2x+B2y+C2=0�ķ�������Ϊ��-B2��A2����
����ֱ��A1x+B1y+C1=0��A2x+B2y+C2=0��ֱ��
��������ֱ�ߵķ���������������Ϊ0��
������-B1��A1����-B2��A2��=0��
�ɵ�A1A2+B1B2=0��
�ʢ���ȷ���ڴ���
��A1B2-A2B1=0��������A1=0��B1=1��A2=0��B2=1��C1=C2����ʱ��ֱ���غϣ����Բ���֣�
��l1��l2�������A1B2-A2B1=0������
���ԡ�A1B2-A2B1=0���ǡ�l1��l2���ı�Ҫ������������ʢ۴���
����-$\frac{{A}_{1}}{{B}_{1}}$=-$\frac{{A}_{2}}{{B}_{2}}$��ʱ����ֱ�߿���ƽ�У�Ҳ�����غϣ��ʳ���Բ�������
��l1��l2ʱ��B1��B2���ܶ�����0���ʡ�-$\frac{{A}_{1}}{{B}_{1}}$=-$\frac{{A}_{2}}{{B}_{2}}$����һ���������ʱ�Ҫ�Բ�������
���ϣ���-$\frac{{A}_{1}}{{B}_{1}}$=-$\frac{{A}_{2}}{{B}_{2}}$����l1��l2�ļȷdz���ַDZ�Ҫ������
�ʢܴ���
�ʴ�Ϊ���٣�
���� ���⿼���������ͱ�Ҫ�������жϣ�Ҫ�������жϳ�������ͱ�Ҫ�����ķ�����
����p⇒qΪ��������q⇒pΪ�����⣬������p������q�ij�ֲ���Ҫ������
����p⇒qΪ��������q⇒pΪ�����⣬������p������q�ı�Ҫ�����������
����p⇒qΪ��������q⇒pΪ�����⣬������p������q�ij�Ҫ������
����p⇒qΪ��������q⇒pΪ�����⣬������p������q�ļ������Ҳ����Ҫ������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $2\sqrt{3}$ | B�� | 4 | C�� | $2\sqrt{6}$ | D�� | $4\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 22 | B�� | 25 | C�� | 31 | D�� | 28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
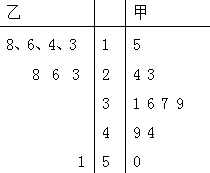 ��֪�ס������������˶�Աijʮ�������÷ֵľ�Ҷͼ��ͼ��ʾ����ס�����������ʮ�������е÷ֵ�ƽ�����뷽��Ĵ�С��ϵΪ��������
��֪�ס������������˶�Աijʮ�������÷ֵľ�Ҷͼ��ͼ��ʾ����ס�����������ʮ�������е÷ֵ�ƽ�����뷽��Ĵ�С��ϵΪ��������| A�� | $\overline{X_��}$��$\overline{X_��}$��S2����S2�� | B�� | $\overline{X_��}$��$\overline{X_��}$��S2����S2�� | ||
| C�� | $\overline{X_��}$��$\overline{X_��}$��S2����S2�� | D�� | $\overline{X_��}$��$\overline{X_��}$��S2����S2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $f��x��=sin��{2x+\frac{��}{3}}��$ | B�� | $f��x��=sin��{2x+\frac{��}{6}}��$ | C�� | $f��x��=sin��{\frac{1}{2}x+\frac{��}{3}}��$ | D�� | $f��x��=sin��{\frac{1}{2}x+\frac{��}{6}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ֱ������ | B�� | ֱ�������� | ||
| C�� | �ȱ������� | D�� | ���������λ�ֱ�������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com