练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
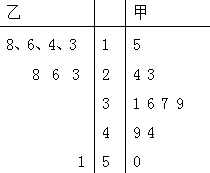
    16．已知甲、乙两名篮球运动员某十场比赛得分的茎叶图如图所示，则甲、乙两人在这十场比赛中得分的平均数与方差的大小关系为（　　）
    A．$\overline{X_甲}$＜$\overline{X_乙}$，S2甲＜S2乙B．$\overline{X_甲}$＜$\overline{X_乙}$，S2甲＞S2乙
    C．$\overline{X_甲}$＞$\overline{X_乙}$，S2甲＞S2乙D．$\overline{X_甲}$＞$\overline{X_乙}$，S2甲＜S2乙

    分析 由茎叶图，分别求出$\overline{{x}_{甲}}$和$\overline{{x}_{乙}}$，由茎叶图知：甲的数据较分散，乙的数所较集中，由此能求出结果．

    解答 解：由茎叶图，得：
    $\overline{{x}_{甲}}$=$\frac{1}{10}$（15+24+23+31+36+37+39+49+44+50）=34.8，
    $\overline{{x}_{乙}}$=$\frac{1}{8}$（18+16+14+13+28+26+23+51）=23.625，
    ∴$\overline{{x}_{甲}}$＞${\overline{{x}_{乙}}}_{\;}$，
    又由茎叶图知：甲的数据较分散，乙的数所较集中，
    ∴${{S}_{甲}}^{2}$＜${{x}_{乙}}^{2}$，
    故选：D．

    点评 本题考查两组数据的平均数、方差的比较，是基础题，解题时要认真审题，注意茎叶图性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．数列{an}满足a1=1，log2an+1=log2an+1，它的前n项和为Sn，则满足Sn＞2015的最小的n值是11．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知等差数列{an}中，a2+a7=6，则3a4+a6=12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．命题：?x＞0，x（x-1）＞0的否定形式为（　　）
    A．?x＞0，x（x-1）≤0B．?x＞0，x（x-1）≤0C．?x≤0，x（x-1）≤0D．?x＞0，x（x-1）＞0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知等差数列{an}的前n项和为Sn，公差d≠0，且S3=6，a1，a2，a4成等比数列．
    （1）求数列{an}的通项公式；
    （2）设${b_n}={2^{a_n}}$，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．对于直线l1：A1x+B1y+C1=0和l2：A2x+B2y+C2=0，下列两个命题中是真命题的为①．
    ①“A1A2+B1B2=0”是“l1⊥l2”充要条件；
    ②“（-$\frac{{A}_{1}}{{B}_{1}}$）•（-$\frac{{A}_{2}}{{B}_{2}}$）=-1”是“l1⊥l2”充要条件；
    ③“A1B2-A2B1=0”是“l1∥l2”的充要条件；
    ④“-$\frac{{A}_{1}}{{B}_{1}}$=-$\frac{{A}_{2}}{{B}_{2}}$”是“l1∥l2”的充要条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．设a=log23，$b=\frac{4}{3}$，c=log34，则a，b，c的大小关系为（　　）
    A．b＜a＜cB．c＜a＜bC．a＜b＜cD．c＜b＜a

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知数列{an}满足a1=1，$\frac{{{a_n}-{a_{n+1}}}}{{{a_n}{a_{n+1}}}}=\frac{2}{n（n+1）}$（n∈N*），则an=$\frac{n}{3n-2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知抛物线y2=2px（p＞0），倾斜角为$\frac{π}{4}$的直线AB过抛物线的焦点F且与抛物线交于A，B两点（|AF|＞|BF|）．过A点作抛物线的切线与抛物线的准线交于C点，直线CF交抛物线于D，E两点（|DF|＜|FE|）．直线AD，BE相交于G，则G点的横坐标为（　　）
    A．$-\frac{{\sqrt{2}p}}{4}$B．$-\frac{p}{2}$C．$-\frac{{\sqrt{3}p}}{2}$D．-p

    查看答案和解析>>

    同步练习册答案