
分析 把已知数列递推式裂项变形,然后利用累加法求得数列{an}的通项公式.
解答 解:由$\frac{{{a_n}-{a_{n+1}}}}{{{a_n}{a_{n+1}}}}=\frac{2}{n(n+1)}$,得$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}=2(\frac{1}{n}-\frac{1}{n+1})$,
∵a1=1,
∴$\frac{1}{{a}_{n}}=(\frac{1}{{a}_{n}}-\frac{1}{{a}_{n-1}})+(\frac{1}{{a}_{n-1}}-\frac{1}{{a}_{n-2}})+…+(\frac{1}{{a}_{2}}-\frac{1}{{a}_{1}})+\frac{1}{{a}_{1}}$
=2[($\frac{1}{n-1}-\frac{1}{n}$)+($\frac{1}{n-2}-\frac{1}{n-1}$)+…+(1-$\frac{1}{2}$)]+1
=2(1-$\frac{1}{n}$)+1=$\frac{3n-2}{n}$,
∴${a}_{n}=\frac{n}{3n-2}$.
故答案为:$\frac{n}{3n-2}$.
点评 本题考查数列递推式,考查了裂项相消法求数列的通项公式,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
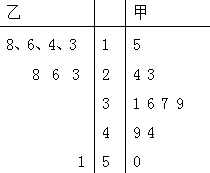 已知甲、乙两名篮球运动员某十场比赛得分的茎叶图如图所示,则甲、乙两人在这十场比赛中得分的平均数与方差的大小关系为( )
已知甲、乙两名篮球运动员某十场比赛得分的茎叶图如图所示,则甲、乙两人在这十场比赛中得分的平均数与方差的大小关系为( )| A. | $\overline{X_甲}$<$\overline{X_乙}$,S2甲<S2乙 | B. | $\overline{X_甲}$<$\overline{X_乙}$,S2甲>S2乙 | ||
| C. | $\overline{X_甲}$>$\overline{X_乙}$,S2甲>S2乙 | D. | $\overline{X_甲}$>$\overline{X_乙}$,S2甲<S2乙 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2013 | B. | 1007 | C. | 2015 | D. | 1009 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
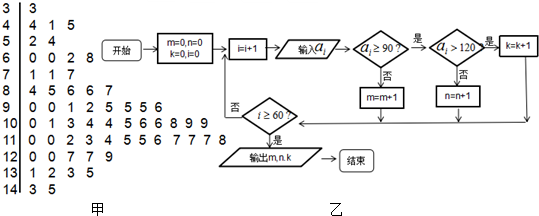
| A. | m=18,n=31,k=11 | B. | m=18,n=33,k=9 | C. | m=20,n=30,k=9 | D. | m=20,n=29,k=11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com