
| A. | $-\frac{{\sqrt{2}p}}{4}$ | B. | $-\frac{p}{2}$ | C. | $-\frac{{\sqrt{3}p}}{2}$ | D. | -p |
分析 令p=2,联立方程组求出A,B,C,D,E的坐标,得出直线AD,BE的方程,求出G点坐标即可.
解答 解:不妨设p=2,抛物线方程为y2=4x,F(1,0),直线AB的方程为y=x-1,
联立方程组$\left\{\begin{array}{l}{y=x-1}\\{{y}^{2}=4x}\end{array}\right.$解得A(3+2$\sqrt{2}$,2+2$\sqrt{2}$),B(3-2$\sqrt{2}$,2-2$\sqrt{2}$),
∵直线AC是抛物线的切线,切点为A,
∴直线AC的方程为y-2-2$\sqrt{2}$=($\sqrt{2}$-1)(x-3-2$\sqrt{2}$),即y=($\sqrt{2}$-1)x+$\sqrt{2}$+1,
又C在抛物线的准线x=-1上,∴C(-1,2),
∴直线CF的方程为y=-x+1,
联立方程组$\left\{\begin{array}{l}{y=-x+1}\\{{y}^{2}=4x}\end{array}\right.$得D(3-2$\sqrt{2}$,2$\sqrt{2}$-2),E(3+2$\sqrt{2}$,-2-2$\sqrt{2}$),
∴A,E关于x轴对称,B,D关于x轴对称,
∴直线AD与直线BE关于x轴对称,
∴G为直线AD与x轴的交点,
∵kAD=$\frac{4}{4\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴直线AD的方程为y-2-2$\sqrt{2}$=$\frac{\sqrt{2}}{2}$(x-3-2$\sqrt{2}$),即y=$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{2}}{2}$,
∴直线AD与x轴的交点为G(-1,0),即G点横坐标为-1.
∴G点横坐标为-$\frac{p}{2}$.
故选:B.
点评 本题考查了直线与抛物线的位置关系,属于中档题.


科目:高中数学 来源: 题型:选择题
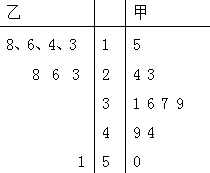 已知甲、乙两名篮球运动员某十场比赛得分的茎叶图如图所示,则甲、乙两人在这十场比赛中得分的平均数与方差的大小关系为( )
已知甲、乙两名篮球运动员某十场比赛得分的茎叶图如图所示,则甲、乙两人在这十场比赛中得分的平均数与方差的大小关系为( )| A. | $\overline{X_甲}$<$\overline{X_乙}$,S2甲<S2乙 | B. | $\overline{X_甲}$<$\overline{X_乙}$,S2甲>S2乙 | ||
| C. | $\overline{X_甲}$>$\overline{X_乙}$,S2甲>S2乙 | D. | $\overline{X_甲}$>$\overline{X_乙}$,S2甲<S2乙 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2013 | B. | 1007 | C. | 2015 | D. | 1009 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
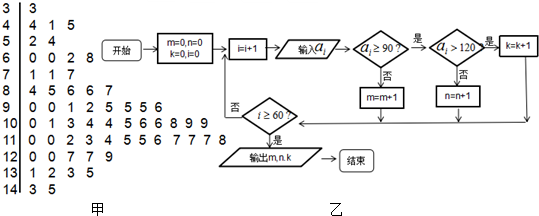
| A. | m=18,n=31,k=11 | B. | m=18,n=33,k=9 | C. | m=20,n=30,k=9 | D. | m=20,n=29,k=11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰直角神经性 | B. | 直角三角形 | ||
| C. | 等边三角形 | D. | 等腰三角形或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}<\frac{1}{b}<0$ | B. | b2>a2 | C. | |b|>|a| | D. | b3>a3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{{\frac{a_1^2+a_2^2+…+a_n^2}{n}}}$ | B. | $\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$ | ||
| C. | $\root{n}{{a}_{1}{a}_{2}…{a}_{n}}$ | D. | $\frac{n}{\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+…+\frac{1}{{a}_{n}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com