
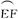 上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在
上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在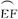 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?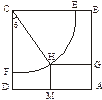
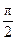 ,Smax=500
,Smax=500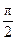 ).
).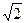 sin(θ+
sin(θ+ ),
),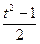 ,且t∈[1,
,且t∈[1,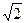 ].
].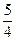 )2+450.
)2+450.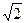 ],∴当t=1时,Smax=500,
],∴当t=1时,Smax=500,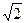 sin(θ+
sin(θ+ )=1
)=1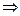 sin(θ+
sin(θ+ )=
)=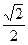 .
. ≤θ+
≤θ+ ≤
≤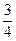 π,∴θ+
π,∴θ+ =
= 或
或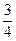 π,
π,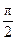 .
.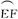 的端点E或F处时,该健身室的面积最大,最大面积是500 m2.
的端点E或F处时,该健身室的面积最大,最大面积是500 m2.

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com