
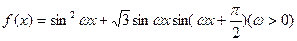
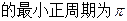 (1)求
(1)求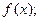
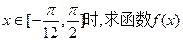 的值域。
的值域。 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:不详 题型:解答题
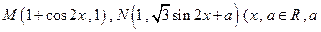 是常数
是常数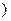 ,令
,令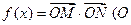 是坐标原点
是坐标原点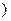 .
.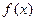 的解析式,并求函数
的解析式,并求函数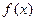 在
在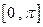 上的单调递增区间;
上的单调递增区间;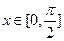 时,
时,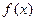 的最大值为
的最大值为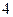 ,求a的值,并说明此时
,求a的值,并说明此时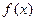 的图象可由函数
的图象可由函数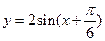 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
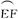 上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在
上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在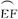 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?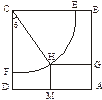
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 求证:m≥5;
求证:m≥5;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com