
| A. | (2,8) | B. | $[2,\frac{17}{4})$ | C. | $(2,\frac{17}{4}]$ | D. | (2,8] |
分析 方程f2(x)-bf(x)+1=0有8个不同实数解,即要求对应于f(x)等于某个常数k,有2个不同的k,再根据函数对应法则,每一个常数可以找到4个x与之对应,就出现了8个不同实数解故先根据题意作出f(x)的简图:由图可知,只有满足条件的k在开区间(0,4]时符合题意.再根据一元二次方程根的分布的理论可以得出答案.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}|lg(-x)|,x<0\\{x^3}-6x+4,x≥0\end{array}\right.$作出f(x)的简图,如图所示: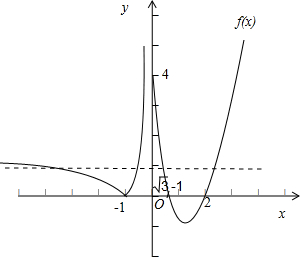
由图象可得当f(x)在(0,4]上任意取一个值时,都有四个不同的x与f(x)的值对应.
再结合题中函数y=f2(x)-bf(x)+1 有8个不同的零点,
可得关于k的方程 k2 -bk+1=0有两个不同的实数根k1、k2,且0<k1≤4,0<k2≤4.
∴应有$\left\{\begin{array}{l}{△={b}^{2}-4>0}\\{0<\frac{b}{2}<4}\\{0-b×0+1>0}\\{16-4b+1≥0}\end{array}\right.$,解得 2<b≤$\frac{17}{4}$,
故选:C.
点评 本题考查了函数的图象与一元二次方程根的分布的知识,采用数形结合的方法解决,使本题变得易于理解.数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷,属于中档题.


科目:高中数学 来源: 题型:解答题
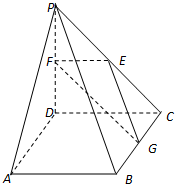 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | r>s>t | B. | r>t>s | C. | s>r>t | D. | s>t>r |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,勘探队员朝一座山行进,在前后两处观察山顶的仰角是30度和45度,两个观察点之间的距离是200m,则此山的高度为100($\sqrt{3}$+1)(用根式表示).
如图,勘探队员朝一座山行进,在前后两处观察山顶的仰角是30度和45度,两个观察点之间的距离是200m,则此山的高度为100($\sqrt{3}$+1)(用根式表示).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com