
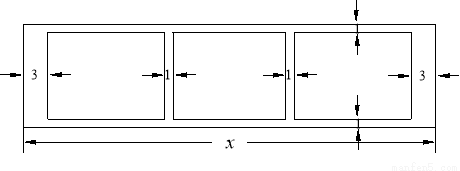
(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为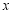 (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为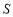 (m2).
(m2).
(1)求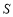 关于
关于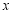 的函数关系式;
的函数关系式;
(2)求 的最大值.
的最大值.
(1)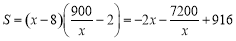 ,
,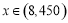 .
.
2)当矩形温室的室内长为60 m时,三块种植植物的矩形区域的总面积最大,最大为 m2 .
m2 .
【解析】
试题分析:(1)建立实际问题函数解析式,关键读懂题意即可,本题题意明确,图形简单,三块种植植物的矩形区域的总面积可看做一个矩形面积: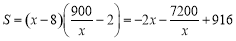 ,根据边长为正得其定义域为
,根据边长为正得其定义域为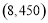
(2)这是一个积为定值的函数,可根据基本不等式求最值: 当且仅当
当且仅当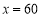 时等号成立.
时等号成立.
试题解析:(1)由题设,得
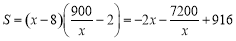 ,
,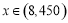 . 6分
. 6分
(2)因为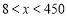 ,所以
,所以 , 8分
, 8分
当且仅当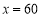 时等号成立. 10分
时等号成立. 10分
从而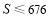 . 12分
. 12分
答:当矩形温室的室内长为60 m时,三块种植植物的矩形区域的总面积最大,最大为 m2 . 14分
m2 . 14分
考点:函数解析式,基本不等式求最值
考点分析: 考点1:函数模型及其应用 试题属性

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:2014-2015学年江苏省常州市高三上学期期末调研测试文科数学试卷(解析版) 题型:填空题
设等比数列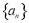 的公比为
的公比为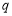 (
(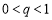 ),前n项和为
),前n项和为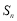 ,若
,若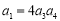 ,且
,且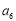 与
与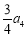 的等差中项为
的等差中项为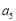 ,则
,则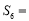 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省常州市高三上学期期末调研测试理科数学试卷(解析版) 题型:填空题
在平面直角坐标系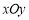 中,已知圆
中,已知圆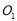 ,圆
,圆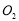 均与
均与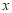 轴相切且圆心
轴相切且圆心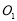 ,
,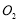 与原点
与原点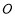 共线,
共线,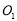 ,
,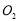 两点的横坐标之积为6,设圆
两点的横坐标之积为6,设圆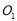 与圆
与圆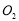 相交于
相交于 ,
,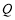 两点,直线
两点,直线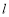 :
: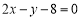 ,则点
,则点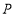 与直线
与直线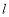 上任意一点
上任意一点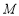 之间的距离的最小值为 .
之间的距离的最小值为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数 ,
, .
.
(1)证明: ;
;
(2)若 在
在 恒成立,求
恒成立,求 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com